Сегодня мне хочется в очередной раз попытаться ответить на вопрос который, наверное, неприятнее всего слышать от школьников, но очень часто его можно услышать и от взрослых людей, зачем вообще нужны эти производные.
Действительно, вопрос очень интересный, особенно для тех, кто учиться сейчас в школе, или давно ее закончил и до сих пор не понимает, зачем его заставляли учить, кахалось бы, бессконечную таблицу производных. В этой статье я попытаюсь вам простыми словами что это, где это, и зачем это существует.
Давайте начнем с самого понятия производная. В школе (по крайней мере в моей) нам дают абсолютно не понятные понятия всех тем математического анализа, включая интеграл, предел, прозводную, дифференцирование и т.д, простыми же словами, или как я люблю обьяснять своим ученикам такие вещи "одним словом", производная это скорость. В каком смысле скорость спросите вы, это скорость роста функции, рассмотрим примеры для большего понимания.
Первый пример. Представим что вы коллекционируете монеты. Каждый месяц вы ходите в ресторан 2 раза. Тогда какая функция будет задавать эти события? Не долго думая мы поймем что это f(y)=x (рис 1).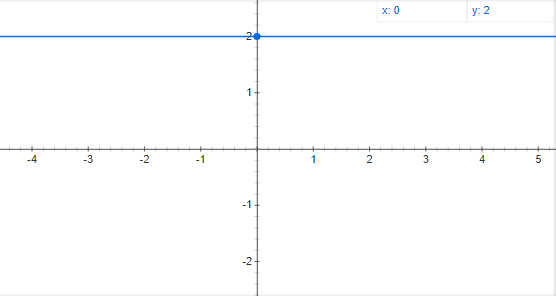
Можем заметить, что график функции и значения y не зависят от временной шкалы х. Как думаете, чему равна проивзодная этой функции? Она равна 0. Доказать это легко, первый вариант это просто взять проивзодную из таблицы производных. Производная константы равна 0, соотвественно y=С, y'=0. И ествественно графически, выше уже было сказано что производная это скорость роста функции, следовательно, если нет роста(что мы видим на графике), нет и скорости роста функции. Здесь я не подошел к решения производных и близко, но важно обьяснить простым языком термин.
Теперь давайте рассмотрим вариант где проивзодная не будет равняться нулю. Предположим что каждый месяц вы увеличиваете колчиество походов в ресторан на 2. Первый месяц вы сходили в ресторан 2 раза, второй месяц 4, третий 6 и так далее. В данном случае эту зависимость будет отображать функция y=2x. Чему равна производная такой функции по таблице, y'=2. Скорость роста функции равна двум.
Теперь же давайте посчитаем наконец производную. Допустим, вы делаете новое ограждение на даче в форме некоего прямоугольника. У вас есть 64 одинаковых отсека для ограждения. Вам нужно посчитать с какой стороной сделать огрождение что бы площадь вашей дачи была наибольшей. Довольно таки необычный пример, но все же он решаеться с помощью производной. Что нам дано? Нам дан периметр, поэтому очень легко описать прямоугольник, где одна сторона будет Х, а вторая 32-Х. Соответственно составляем уравнение где площадь:
- S=(32-х)*х. Отсюда S=32х-х^2. Давайте же найдем производную данной функции. y=32x-x^2, y'=32-2x. Приравниваем наше уравнение к нулю и получаем что х=16. Следовательно наибольшая площадь прямоугольника имеющего периметр 64 будет со стороной 16. А если уточнить то это будет квадрат со стороной 16. Такой себе пример скажите вы, кому нужно сторить ограждение для дачи. Возможно, также производная используется для анализа экономических стратегий. Зная основное свойство производной - показывает скорость роста функции, можно интегрировать ее в анализ тех или иных временых промежутков. К примеру следуя стратегии А, компания имела прибыль которая характеризовалась функцией f(y)=x, следуя же стратегии В компания имела прибыль которая характеризуется функцией p(y)=x. Не берите в внимание названия функций, они могут быть совершенно любые. Как узнать без больших расчетов, расчетов базовой и относительной динамики прибыли за исследуемый период времени, какая стратегия эффективнее? Естественно путем нахождения производной если p'(y)=x больше f'(y)=x соотвественно скорость роста функции p(y)=x выше, и рост прибыли выше. Конечно, использовать слепо производные в анализе не стоит, ведь прибыль то может быть и меньше, но быстрее рости, в даном случае стратегия будет возможно менее эффективной.
Подведем итоги, проивзодная в общем понимании - скорость роста функции. Производные могут использоваться как в строительстве ограждений для ваших дач, так и для анализа экономическиъ стратегий, последнее особенно важно если вы собираетесь в дальнейшем связывать свою жизнь и образование со сферой экономики.





