Низка вузів Австрії, зокрема, Віденський технічний університет пропонують безкоштовне навчання для українців. Для цього потрібно підтвердити знання німецької мови, пройти підготовчі курси та здати екзамен. Слід мати на увазі, що на екзамені з математики у Відні вас очікуватимуть задачі з математичного аналізу, які виходять за рамки української шкільної програми. Багато з тих тем, які вам потрібно знати, щоб успішно скласти цей екзамен, в Україні вивчаються на першому курсі в університетах (в школах ці теми не вивчають). Тому слід ретельно готуватись до вступного екзамену. Поговоримо про те на які саме теми слід звернути увагу та як готуватись.
По-перше, абітурієнти в Австрії повинні вміти проводити повне дослідження функції, тобто знаходити точки екстремуму, точки перегину функції, проміжки зростання, спадання, опуклості, угнутості функції, вміти знаходити рівняння асимптот функції. Під час підготовки варто звернути увагу на термінологію. Наприклад, Wendepunkt – точка перегину функції, Tangente – дотична, а тому Wendetangente – це дотична, проведена в точці перегину функції. Часто на вступних екзаменах у Віденському технічному університеті трапляються задачі, у яких вас просять знайти Funtionsterm. Цей вираз, мабуть, не має дослівного перекладу українською, але коли ви його бачити, то слід розуміти, що вас просять з’ясувати який вигляд має функція. Приміром, на одному з екзаменів була така задача:
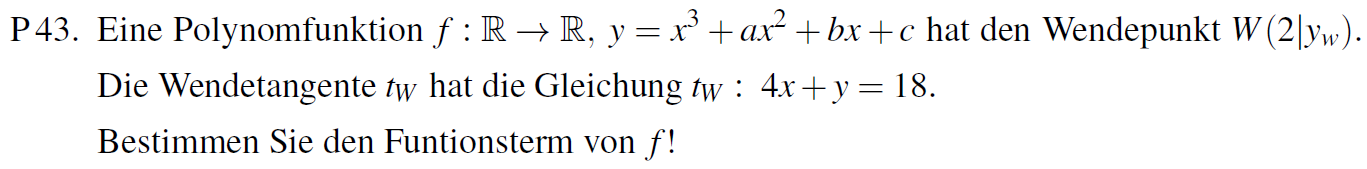
Точка W з абсцисою рівною 2 є точкою перегину функції у=х³+ах²+bх+с. Дотична, проведена до графіка цієї функції у точці W має рівняння 4х+у=18. Необхідно знайти Funtionsterm, тобто фактично знайти значення параметрів a, b та с. Насамперед, точка W має координати W(2; 8+4a+2b+c). Перша похідна y´=3x²+2ax+b. Друга похідна y´´=6x+2a. Тому в точці W значення другої похідної дорівнює 12+2а. Але W – точка перегину. Тому 12+2а=0, звідки а= –6. Тоді W(2; –16+2b+c). Оскільки, y´=3x²+2ax+b, то кутовий коефіцієнт дотичної, проведеної в точці W, дорівнює k=12+4a+b. Тоді рівняння цієї дотичної у–(–16+2b+c)= (12+4a+b)(х–2), звідки у= (12+4a+b)х–40–8а+с. Але а= –6. Тому рівняння дотичної у= (b–12)х+8+с. Порівнюючи це рівняння з рівнянням з умови задачі у= –4х+18, отримаємо, що b–12= –4 та 8+с=18, звідки b=8, с=10. Отже, Funtionsterm у=х³–6х²+8х+10.
Більше того, абітурієнти повинні, навіть, знати означення сідлової точки функції однієї змінної (це поняття, навіть, не завжди в українських університетах розглядається, не говорячи вже про школи). Сідлова точка – це така точка перегину функції, у якій і перша і друга похідна одночасно дорівнюють нулю, але ця точка не є точкою екстремуму. Наприклад, точка (0; 0) є сідловою точкою функції у=х³, бо y´(0)=0 та y´´(0)=0 і точка (0; 0) є точкою перегину функції у=х³. Приміром, на екзамені була така задача про сідлову точку (Sattelpunkt):
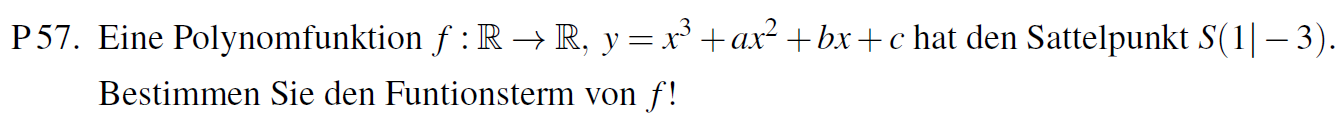
Також абітурієнти у Відні повинні вміти шукати границі, що не вивчається в українських школах. Приміром, ось такі границі:

Як бачимо, щонайменше слід знати чудові границі та вміти їх застосовувати до розв’язання задач. Але не завадять знання і правила Лопіталя.
Щоб добре здати вступний екзамен, потрібно також добре володіти методами інтегрування, наприклад, методом інтегрування частинами, який в Україні не вивчається у звичайних школах.
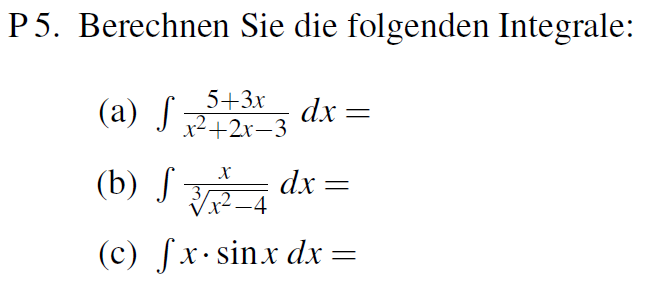
Потрібно вміти обчислювати об’єми тіл обертання, утворених обертанням фігур, обмежених графіками функцій, і до того ж для випадків, коли обертання відбувається як навколо осі абсцис, так і навколо осі ординат.

З алгебри потрібно знати рівняння площини у тривимірному просторі, що теж не вивчається в українських школах на рівні стандарту. Приміром, у пункті (а) наступної задачі нас просять записати рівняння площини трикутника АВС (координати вершин трикутника відомі):

І ще чимало інших тем з вищої математики потрібно буде вивчити, щоб успішно вступити у Віденський технічний університет. Ці теми, безумовно, розглядатимуться на підготовчих курсах, але враховуючи те, що ці курси відбуваються німецькою мовою, варто заздалегідь ознайомитись з цими темами.





