Итак, явление передачи тепловой энергии изучается в 8 классе, затем к этой теме возвращаются в 10 классе. Для того, чтобы решать подобные задачи, прежде всего выясним для себя несколько основных моментов:
- Любые переходы в разные агрегатные состояния сопровождаются дополнительными очень большими теплозатратами на сам процесс (испарение, например)
- Тепловая энергия - это один из видов ЭНЕРГИИ в общей системе физики, поэтому для нее также свойственны переходы в кинетическую/потенциальную
- С точки зрения задач на мощность и КПД нагревательных устройств следует считать энергию, которая идет на нагрев собственно вещества в устройстве как полезную работу. Тепловую энергию, образующуюся при, например, сгорании вещества следует считать общей работой/энергией (в разрезе задач с КПД)
Простейшая задача такого типа характеризуется только заданным изменением температуры вещества без изменения его агрегатного состояния:

На подобных задачах не вижу смысла останавливаться - они вполне решаются с помощью указанной в задаче формулы. Интереснее становится, когда тело меняет агрегатное состояние. В таком случае все количество теплоты условно разбивается на отдельные части, каждая из которых вычисляется по соответствующей формуле. Например превращение воды температурой 20 градусов в пар температурой 150 градусов рассчитывается по промежуточной формуле Q(полная)= Q(нагрев воды до 100 градусов)+ Q(испарение) + Q(нагрев пара до 120 градусов)
Также обратим внимание, что при переходе в другое агрегатное состояние, у вещества изменяются определенные характеристики, например удельная теплоемкость. Поэтому q для пара и воды следует смотреть в таблице отдельно.
Подобные задачи могут решаться с применением графика. На таком графике промежутки постоянства - это промежутки, во время которых предоставляемая теплота уходит на изменение агрегатного состояния вещества. Вот пример подобной задачи на нагревание воды и превращение ее в пар
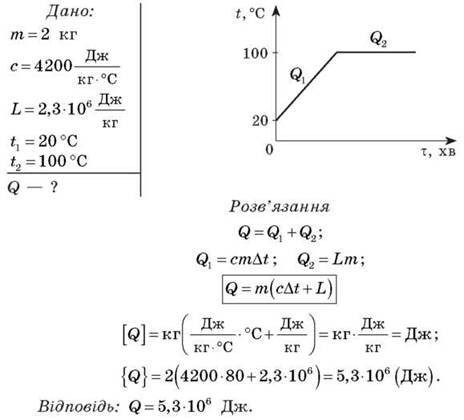
Если речь идет о разных веществах (не путать с разными агрегатными состояниями одного вещества), то скорее всего мы имеем уравнение на тепловой баланс. При заданных идеальных условиях вся теплота остается между двумя веществами, поэтому количество теплоты, которое отдает одно, равно количеству теплоты, которое принимает другое. Пользуясь уже известными формулами и используя баланс для приравнивания количества теплоты решаем подобную задачу следующим образом

Ну и последний существенный случай - задачи на КПД. Как я уже писал выше, просто следует разграничить теплоту полезную, то есть работу (на нагрев собственно вещества) и теплоту общую (например ту теплоту, что образуются при сгорании топлива). Зная массу топлива и переданное количество теплоты веществу можно найти КПД устройства следующим образом:
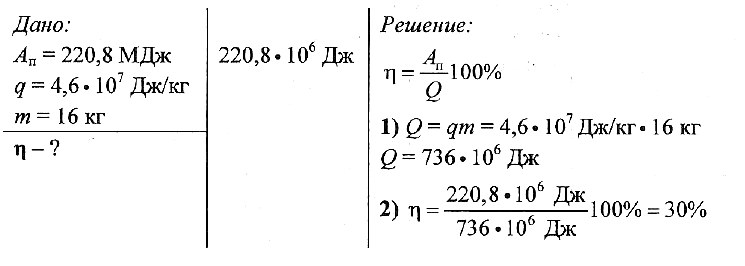
Пользуясь данными советами подобные задачи перестанут нести в себе сложность и станут более интересными. Успехов в учебе и в жизни!





