Існує міф про те нібито в Європі вступні екзамени простіші за наше ЗНО. Однак, часто-густо ситуація може бути повністю протилежною. Для прикладу, розглянемо завдання матури-2022 (це польський аналог нашого ЗНО) профільного рівня з математики. Як ви зможете переконатись, завдання нашого ЗНО є простішими.
Задача №10. Нехай а₁, а₂, … – нескінченна геометрична прогресія, всі члени якої є додатними дійсними числами, а b₁, b₂, … – арифметична прогресія. Відомо, що сума всіх членів нескінченної геометричної прогресії а₁, а₂, … дорівнює сумі перших 25-ти членів прогресії b₁, b₂, … До того ж, а₃=b₄, а₁=675, а₂₂=(5/4)а₂₃+(1/5)а₂₁. Слід обчислити b₁.

Нехай q – знаменник прогресії а₁, а₂, …, а d – різниця прогресії b₁, b₂, …. З умови випливає, що 0<q<1. Матимемо, що а₁q²¹=(5/4)а₁q²²+(1/5)а₁q²⁰, звідки q=(5/4)q²+1/5, звідки q²–0,8q+0,16=0, звідки (q–0,4)²=0, звідки q=0,4. Тоді а₁+а₂+…=а₁/(1–q)= а₁/0,6=675/0,6= 1125. Тоді b₁+b₂+…+b₂₅=1125. Тому 25(b₁+b₂₅)/2=1125, звідки b₁+b₂₅=90. Також матимемо, що а₃= а₁q²= 675∙(0,4)²=108. Тоді b₄=108. Тоді b₁+3d=108, звідки d=36 – b₁/3. Але b₁+b₂₅=90. Тому 2b₁+24d=90. Тоді 2b₁+24(36 – b₁/3)=90, звідки b₁=129.
Тепер розв’яжемо рівняння (sinx)+(sin2x)+(sin3x)=0 на відрізку [0; π]. Оскільки, (sinx)+(sin3x)= 2(sin2x)(cosx), то задане рівняння набуде вигляду: (sin2x)(1+2cosx)=0. Отже, sin2x=0 або 1+2cosx=0. Розв’язок рівняння sin2x=0 має вигляд х= πn/2, n є Z, а тому на відрізку [0; π] маємо корені х=0, х= π/2 та х=π. Рівняння 1+2cosx=0 рівносильне рівнянню cosx= –0,5, а тому х= ±2π/3+2πn, n є Z, а тому на відрізку [0; π] маємо корінь х=2π/3.

У 12-ій задачі необхідно знайти всі дійсні значення параметра m, за яких рівняння х²–(m+1)x+m=0 має два різні дійсні корені х₁ та х₂ такі, що х₁≠0, х₂≠0 та (1/х₁)+(1/х₂)+2=(1/х₁)²+(1/х₂)². Дискримінант D=(m+1)²–4m=(m–1)². Для того, щоб задане рівняння мало два різні дійсні корені, необхідно і достатньо, щоб (m–1)²>0, що рівносильно m≠1. Неважко знайти і самі корені заданого рівняння: х₁=m та х₂=1. Тоді m≠0, бо за умовою, х₁≠0. Тоді 1+(1/m)+2=1+(1/m²), звідки 2m²+m–1=0. Рівняння 2m²+m–1=0 має два корені: m= –1 та m=0,5. Обидва ці корені задовольняють умови m≠0 та m≠1.
У 13-ій задачі необхідно обчислити висоту h прямої призми, основою якої є прямокутник ABCD. Відомо, що площа трикутника AFH дорівнює 26,4 та, що sinα =12/13, де через α позначено кут HAF і відомо, що цей кут є гострим (див.рис).
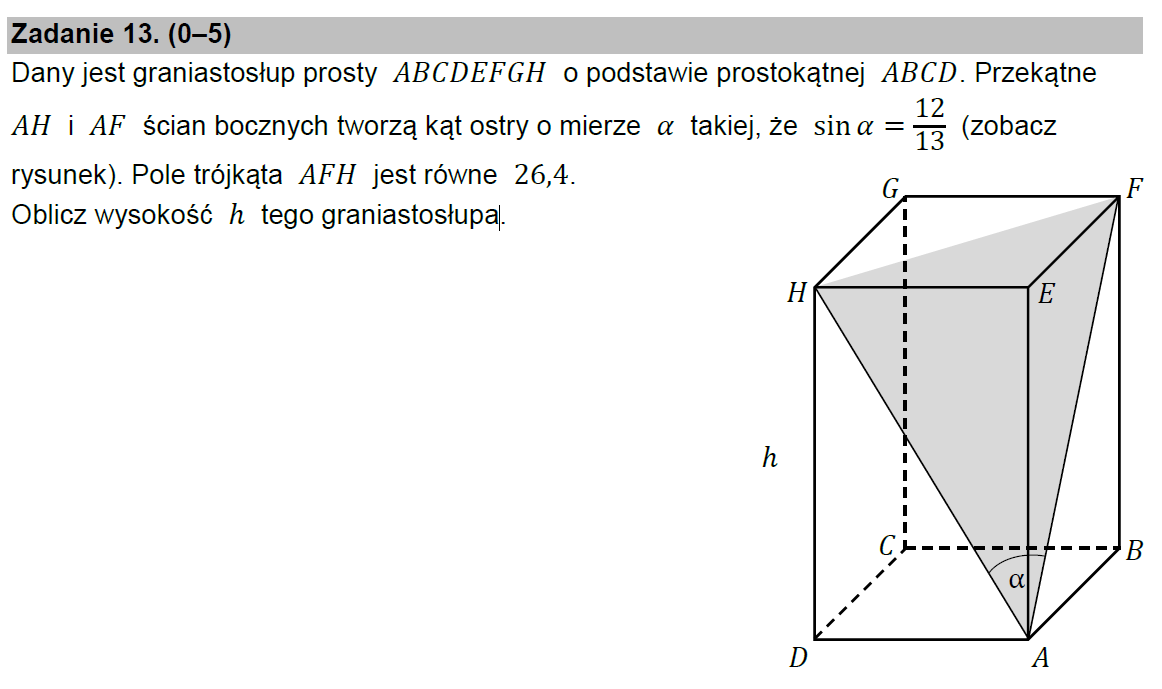
Тоді 0,5∙AH∙AF∙sinα =26,4, звідки AH∙AF=57,2. Оскільки, sinα = 12/13, то cos²α=1– sin²α= 1–144/169= 25/169. Оскільки, кут α гострий, то cosα= 5/13. За теоремою косинусів, для трикутника AFH матимемо, що HF²=AH²+AF²–2AH∙AF∙cosα, звідки HF²=AH²+AF²–2∙57,2∙5/13, звідки HF²=AH²+AF²–44. Для зручності, позначимо AB=a, AD=b. Тоді AH²=h²+b², AF²=h²+а², HF²= а²+b². Тоді а²+b²=(h²+b²)+(h²+а²)–44, звідки 2h²=44, звідки h= √̅2̅2.
Задача №14. АВС – рівнобедренний трикутник (АС=ВС), площа якого дорівнює 15. Координати точки А(–3; 2). Сторона ВС лежить на прямій, рівняння якої у=х–1. Необхідно знайти координати вершин В та С.

Пряма ВС (у=х–1) утворює кут 45° з віссю абсцис. Тому вектор В̅С̅ є колінеарним з вектором s̅(1; 1), адже вектор s̅ (1; 1) з віссю абсцис теж утворює кут рівний 45°. Нехай точка С має абсцису рівну х₀. Тоді її ордината рівна у₀=х₀–1. Тобто С(х₀; х₀–1). Тоді координати вектора А̅С̅(х₀+3; х₀–3). Нехай γ – кут між векторами А̅С̅(х₀+3; х₀–3) та s̅ (1; 1). У такому випадку кут γ дорівнює або внутрішньому куту С або зовнішньому куту С трикутника АВС. В обох цих можливих випадках sinγ =sinﮮАСВ. Довжина вектора s̅ (1; 1) дорівнює √̅2̅ , а довжина вектора А̅С̅(х₀+3; х₀–3) дорівнює √((х₀+3)²+(х₀–3)²) = √(2(х₀)²+18). Тому |s̅|∙|А̅С̅|=2∙√((х₀)²+9). Скалярний добуток векторів s̅ та А̅С̅ дорівнює 1∙(х₀+3)+1∙(х₀–3)=2х₀. Тому для кута γ між цими векторами матимемо, що cosγ=2х₀/(2∙√((х₀)²+9)) =х₀/√((х₀)²+9). Тоді sin²γ=1–cos²γ =1–(х₀)²/((х₀)²+9)= 9/((х₀)²+9). Оскільки ж, sinγ>0, то sinγ=3/√((х₀)²+9). Отже, sinﮮАСВ =3/√((х₀)²+9). Для зручності, позначимо АС=ВС=а. Тоді площа трикутника АВС дорівнює S=0,5а²sinﮮАСВ= 0,5а²∙3/√( (х₀)²+9 )= 1,5а²/√( (х₀)²+9 ). Але а=√(2(х₀)²+18). Тоді S=1,5(2(х₀)²+18)/√((х₀)²+9)= 3∙√((х₀)²+9). Але S=15. Тому 3∙√((х₀)²+9)=15, звідки (х₀)²+9=25, звідки х₀= ±4. Отже, точка С має координати С(4; 3) або С(–4; –5). В обох цих випадках довжина сторони АС дорівнює √(2(х₀)²+18)=5√̅2̅ . Зауважимо, що цей результат можна було отримати й іншим методом. Можна було спочатку записати рівняння висоти АН трикутника АВС (Н є ВС). Її рівняння у–2= –(х+3). Далі можна було знайти координати точки Н, як точки перетину прямих у–2=–(х+3) та у=х–1. Маючи координати точок А та Н, можна було знайти довжину висоти АН. Маючи ж довжину висоти АН та площу трикутника АВС, можна було знайти довжину сторони ВС. Але АС=ВС. Знаючи довжину сторони АС та те, що АС=√( 2(х₀)²+18 ), можна було знайти х₀. Тепер нехай В(х₁; х₁–1). Тоді: а) Якщо С(4;3), то СВ²=(х₁–4)²+(х₁–4)²=2(х₁–4)². Але СВ²=50. Тому (х₁–4)²=25, звідки х₁=9 або х₁= –1. Тоді В(9; 8) або В(–1; –2). б) Якщо С(–4; –5), то СВ²=(х₁+4)²+(х₁+4)²=2(х₁+4)². Але СВ²=50. Тому (х₁+4)²=25, звідки х₁=1 або х₁= –9. Тоді В(1; 0) або В(–9; –10). Отже, є чотири варіанти: 1) С(4;3), В(9; 8); 2) С(4;3), В(–1; –2); 3) С(–4; –5), В(1; 0); 4) С(–4; –5), В(–9; –10). Неважко переконатись, що всі ці варіанти задовольняють умову задачі.

Розглядаємо всі рівнобедренні трикутники, периметр яких дорівнює 18.
а) Доведіть, що площа S кожного такого трикутника є функцією довжини b його бічної сторони, причому S(b)=0,5(18–2b)√̅(̅1̅8̅b̅–̅8̅1̅) .
б) Знайдіть область визначення функції S(b).
в) Серед таких трикутників знайдіть той, площа якого найбільша, та обчисліть його сторони.
Пропоную вам останню задачу розв’язати самостійно.





