Параллельные переносы и преобразования графиков функций являются одной из важнейших тем курса школьной алгебры. Обычно перенос вдоль оси OY(вверх/вниз) не вызывает трудностей в понимании, поскольку именно представление функции y=f(x) как y=f(x)+a является интуитивно логичным.
Вопросы у учащихся начинаются, когда дело доходит до параллельного переноса графика функции вдоль оси OX (вправо/влево).
Правило: график функции y=f(x+a) образуется параллельным переносом графика функции y=f(x) на пунктов вдоль оси OX:
- вправо, если a<0;
- влево, если a>0.
Путаница возникает, когда учащиеся хотят для получения графика функции y=f(x+1) смещать график y=f(x) на 1 пункт вправо, аргументируя свои соображения операцией сложения (+1) к аргументу, а функцию y=f(x -1) получать переносом графика y=f(x) на 1 пункт влево, поскольку присутствует вычитание (-1).
Проанализируем, почему такая логика не работает при параллельном переносе вдоль оси OX.
Объяснение
Проиллюстрируем преобразование точек графика при увеличении аргумента x в 2 единицы на примере прямой y=2x.
Возьмем любые две точки, например x=0 и x=1, и найдем значения обеих функций в них. Внесем полученные значения в таблицу. По полученным координатам точек построим две прямые.
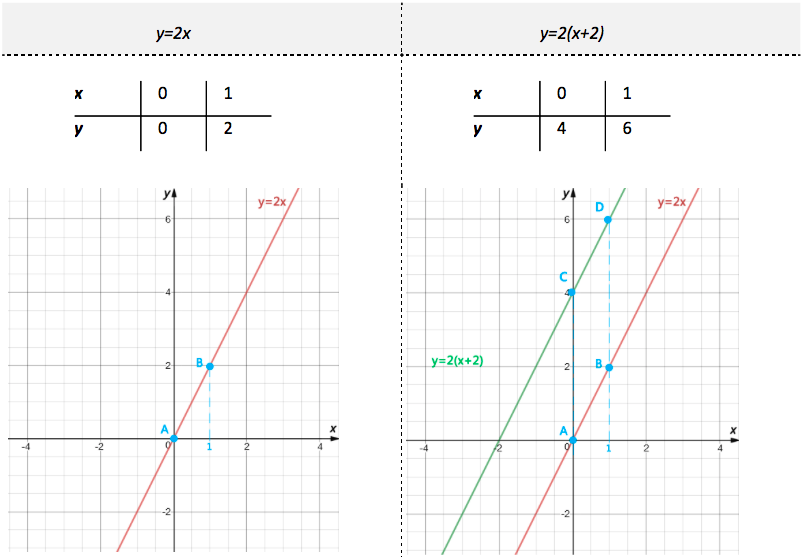
Как видно из графиков, точки C и D графика функции y=2(x+2), при тех же значениях абсцисс (x), что и для функции y=2x, имеют отличные от них значения ординат (y).

Поскольку мы рассматриваем параллельный перенос графика вдоль оси OX, его точки не должны смещаться вдоль оси OY, то есть ординаты точек должны оставаться неизменными. Теперь найдем, на сколько должно измениться значение аргумента функции y=2(x+2), чтобы ординат точек C и D совпал со значением ординат точек A и B

Следовательно, искомые точки будут
A1(-2; 0),
B1(-1; 2)
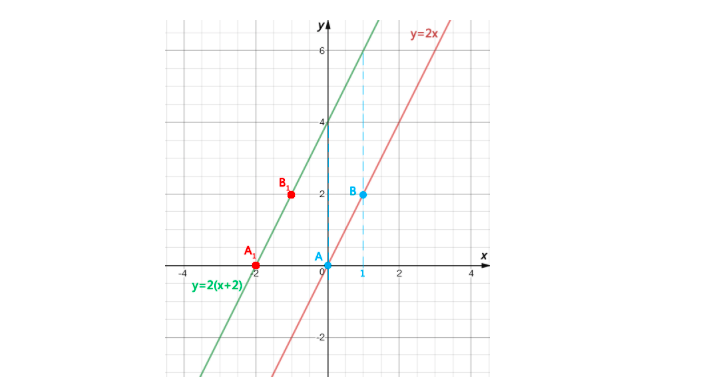
Как видим, график функции y=2(x+2) образовался параллельным переносом графика функции y=2x на 2 пункта влево вдоль оси OX.





