Всі ми можемо допустити помилки, оскільки ніхто з нас не є ідеальним. Але важливо передбачити можливі проблеми заздалегідь та вчитися на чужих помилках, щоб уникнути болісного досвіду власних помилок. Як кажуть, попереджений озброєний. Тому, розгляньмо декілька поширених помилок, які зустрічаються при розв’язанні різноманітних математичних задач.
1. Передчасне скорочення
Одна з найпоширеніших помилок при спрощенні раціональних виразів - це плутання пріоритетів дій. Наприклад, в першій дробі потрібно спочатку додати чисельники, а потім ділити на знаменники. А поки додавання не буде здійснене, доти скорочувати частину чисельника і знаменника ні в якому разі не можна.
Часткове скорочення чисельника і знаменника можна здійснити лише у тому випадку, коли замість знака додавання стоїть знак множення. У такому випадку всі дії мають однаковий пріоритет, тому можна спочатку розділити частину чисельника на знаменник, а потім перемножити результат з рештою чисельника.
Щоб запам'ятати цей момент, можна використовувати таку мнемонічну фразу: "знаки плюс і мінус забороняють скорочувати дріб". Знання цих правил допоможе уникнути багатьох поширених помилок при вирішенні розв’язанні задач.
2. Інтуїція - ворог математики

Це одна з тих формул, яку часто застосовують помилково при розв'язанні математичних задач. Щоб переконатися, що формула застосована правильно, достатньо підставити числа 1 і 1 замість літер "a" та "b" і перевірити результат. Якщо ми використаємо неправильну формулу, то отримаємо (1+1)² = 1² + 1², або 4=2, що свідчитиме про допущену помилку.
Щоб запам'ятати цей момент, можна скористатися наступною запам'ятовувальною фразою: "не можна просто так взяти і закинути квадрат у дужки".
3. Корінь vs квадрат

Часто учні та студенти допускають помилку, коли намагаються спростити вирази, що містять квадратний корінь. Корінь та квадрат є оберненими операціями, тому здається логічним спробувати взаємознищити їх. Проте в більшості формул використовується арифметичний квадратний корінь, який є строго додатною величиною. Якщо параметр "a" є від'ємним числом, невірне добування кореня (за першою формулою) призведе до неправильного результату. Спробуйте підставити в першу (невірну) формулу замість параметра "a" значення "-1". Вийде "1 = -1", що виглядає досить дивно... Використання модуля гарантує, що права частина формули буде додатною.
Для запам'ятовування цього правила можна використовувати таку фразу: "корінь з квадрату - це модуль числа".
4. Куди ж летить галка нерівності?
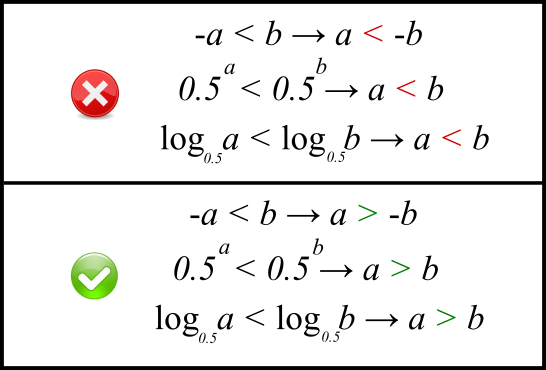
Можна стверджувати, що зміна знаку нерівності на протилежний є однією з найбільш поширених помилок при розв’язанні раціональних, показових і логарифмічних нерівностей.
У випадку раціональних нерівностей необхідно пам'ятати, що множення або ділення на від'ємне число супроводжується зміною знаку нерівності на протилежний. Загальна рекомендація полягає в тому, щоб діяти максимально обережно, помічаючи від'ємні вирази в нерівностях. Ба більше, свої дії завжди можна перевірити на конкретному числовому прикладі. Дійсно, якщо ми хочемо перенести знак «-» з одного боку нерівності на інший (тобто помножити нерівність на -1), то можна записати наперед правильну нерівність: ‑1 < 2. Тепер, проведемо зазначену операцію - перенесемо знак «-» на інший бік. Бачимо, що нерівність залишиться правильною тільки якщо ми «розвернемо» знак нерівності: 1 > -2. Це й підказує нам правильний шлях і для більш складної раціональної нерівності.
У другому та третьому випадках (показникові та логарифмічні нерівності) слід приділяти особливу увагу основі степеня або логарифма в той момент, коли "степені спускаються вниз" або "знімається логарифм". Якщо основа менше одиниці, то знак нерівності змінюється на протилежний. Знайомство з вказаними функціями (вони детально вивчаються в 11 класі) дозволяє перевіряти ці операції на конкретних числових прикладах, як то 0.5² < 0.5¹, але 2 > 1, тобто "спускаючи степені" знак "<" слід замінити на знак ">", щоб нерівність залишалася правильною.
5. А чи існує розв'язок?

Останній приклад стосується теми старшої школи, а саме – теми «тригонометричні рівняння». Для їх розв’язання існують складні формули, які можна зрозуміти та запам'ятати. Проте, перш ніж застосовувати ці формули, корисно згадати, що значення функцій синус та косинус обмежені інтервалом від -1 до 1 за визначенням. Тому якщо у рівнянні зустрічається синус (або косинус), який виходить за цей інтервал, то рівняння просто не має розв'язків.
Отже, перед тим, як записувати розв'язок для тригонометричного рівняння, корисно запитати себе: "Можливо, розв'язків взагалі не існує?"
Висновок
В цій статті були наведені приклади найпоширеніших помилок, які допускаються у математиці. А які складнощі у математиці найчастіше трапляються вам? Поділіться своїм досвідом у коментарях!





