На відміну від НМТ минулого року, на НМТ-2023 вже буде рівняння з параметром, про що свідчить, зокрема, демонстраційний варіант цього тесту. Таке рівняння, очевидно, істотно відрізнятиметься від рівнянь з параметрами, які траплялись на ЗНО, оскільки передбачає коротку відповідь на питання (під час розв’язування таких задач на ЗНО необхідно було наводити розгорнуту відповідь). А це означає, що можна очікувати, що рівняння з параметром на НМТ буде простішим, ніж на ЗНО. Тим не менше, такі задачі викликають труднощі у багатьох учнів. Тому спочатку розглянемо задачу з демонстраційного варіанту НМТ, а потім розв’яжемо ще кілька рівнянь з параметрами.

ОДЗ: x>0. Очевидно, що варто почати із заміни t=log₂ x. Тоді наше рівняння набуде вигляду t²–(a–1)t–a=0. Корені останнього рівняння можна знайти як за допомогою дискримінанта, так і по теоремі Вієта: t₁+t₂=a–1, t₁t₂= –a. Тому t₁= –1, t₂=a. Якщо t= –1, то log₂ x= –1 і тоді х=0,5. Однак корінь х=0,5 не належить проміжку (30; 100). Тому цьому проміжку повинен належати другий корінь нашого рівняння, тобто корінь, який ми отримуємо при t=a. Цей корінь знайдемо із рівняння log₂ x=а, звідки х=2ª. Тоді, враховуючи сказане і умову задачі, 30<2ª<100. Неважко бачити, що найменше ціле а, за якого виконується остання подвійна нерівність, дорівнює 5.
Потренуємось на інших рівняннях з параметрами. Визначте найбільше дійсне значення параметра а, за якого корінь рівняння
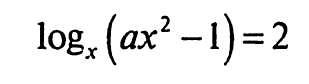
належить проміжку [2; +∞).
ОДЗ: х>0, x≠1 ,ax²>1. Матимемо, що logₓ(ax²–1)=logₓ x². Тоді ax²–1=x², звідки (а–1)x²=1. Отже, а≠1 і тоді x²=1/(а–1). Тому а>1, бо інакше останнє рівняння немає дійсних коренів. Оскільки, х>0 та x²=1/(а–1), то х=1/√̅а̅–̅1. За умовою задачі х≥2. Тому 1/√̅а̅–̅1≥2. Оскільки, обидві частини останньої нерівності є додатними дійсними числами при довільних допустимих значеннях параметра а (а>1), то піднісши до квадрату обидві частини цієї нерівності, отримаємо рівносильну (при а>1) їй нерівність: 1/(а–1)≥4. Оскільки, а–1>0, то помноживши останню нерівність на а–1, отримаємо: 1≥4(а–1), звідки 4a≤5, звідки а≤1,25. Неважко переконатись, що при а=1,25 задане рівняння має корінь х=2. Відповідь: 1,25.
Визначте найбільше ціле значення параметра а, за якого рівняння
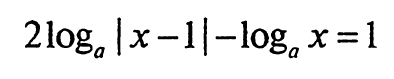
має два дійсні корені, сума квадратів яких дорівнює 23.
ОДЗ: a>0, a≠1, x>0, |x–1|>0 (остання нерівність рівносильна х≠1). Перепишемо наше рівняння у вигляді: logₐ(x–1)² – logₐ x=1, звідки logₐ((x–1)²/x)=1. Тоді (x–1)²/x=а, звідки (x–1)²=ах, звідки х²–(а+2)х+1=0. Дискримінант D=(а+2)²–4=а²+4а=а(а+4). Тоді а(а+4)≥0, звідки методом інтервалів отримаємо, що а є (–∞; –4]U[0; +∞). Враховуючи ж ОДЗ (a>0, a≠1), отримаємо, що а є (0; 1)U(1; +∞). Тобто для всіх а є (0; 1)U(1; +∞) існують корені рівняння х²–(а+2)х+1=0 та а задовольняє ОДЗ. При цьому виконується умова з ОДЗ, що х≠1 (бо якщо х=1, то з рівняння х²–(а+2)х+1=0 випливає, що а=0, але a>0). При цьому (при а>0) також виконується і умова ОДЗ, що x>0, бо якщо поглянути на рівняння х²–(а+2)х+1=0, то по теоремі Вієта видно, що додатними є і добуток і сума коренів цього рівняння, а отже обидва корені цього рівняння додатні. Оскільки, при а є (0; 1)U(1; +∞) існують корені рівняння х²–(а+2)х+1=0, то можемо скористатись теоремою Вієта: : х₁+х₂=a+2, х₁х₂=1. Скористаємось тотожністю (х₁)²+(х₂)²= (х₁+х₂)²–2х₁х₂. Отримаємо, що (х₁)²+(х₂)²=(a+2)²–2. За умовою задачі, (х₁)²+(х₂)²=23. Тому (a+2)²–2=23, звідки (a+2)²=25, звідки а=3 або а= –7. Але a≠ –7, бо а є (0; 1)U(1; +∞). Отже, а=3.
Знайдіть суму найбільшого цілого та найбільшого дійсного значення параметра а, при яких рівняння
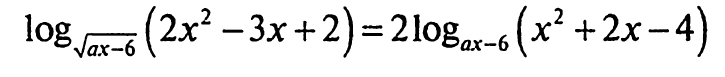
має єдиний розв’язок.
ОДЗ: ax–6>0, ax–6≠1, 2x²–3x+2>0, x²+2x–4>0. Многочлен 2x²–3x+2 не розкладається на множники, бо дискримінант D= –7<0. Тому нерівність 2x²–3x+2>0 виконується для довільного дійсного х. Для многочлена x²+2x–4, знайшовши дискримінант D=20, зможемо розкласти його на множники x²+2x–4=(х+1+√5)(х+1–√5). Тоді за допомогою методу інтервалів розв’язавши нерівність x²+2x–4>0, отримаємо: х є (–∞; –1–√5)U(–1+√5; +∞). Отже, ОДЗ: ax>6, ax≠7, х є (–∞; –1–√5)U(–1+√5; +∞). Перепишемо задане в умові рівняння у вигляді 2logₐₓ₋₆ (2x²–3x+2)= 2logₐₓ₋₆ (x²+2x–4), звідки logₐₓ₋₆ (2x²–3x+2)= logₐₓ₋₆ (x²+2x–4), звідки 2x²–3x+2= x²+2x–4, звідки x²–5x+6=0, звідки х₁= 2, х₂= 3. Обидва корені х₁= 2, х₂= 3 належать проміжку (–1+√5; +∞), бо –1+√5<2. Однак, за умовою задачі, рівняння повинно мати лише один корінь. Тому один з коренів х₁= 2 чи х₂= 3 не повинен задовольняти умови ax>6, ax≠7. Звідси видно, що якщо а≤0, то рівняння немає жодного кореня, бо коренями можуть бути лише додатні числа х₁= 2 та х₂= 3, а тому при а≤0 матимемо, що ах≤0, але має виконуватись умова ax>6. Отже, a>0. Тоді умову ax>6 можна переписати у вигляді x>6/а. Тому, якщо 2>6/а, що рівносильно а>3, то обидва корені х₁= 2 та х₂= 3 будуть задовольняти умову x>6/а, а тому при а>3 рівняння може мати єдиний корінь лише за умови, що 2a=7 або 3а=7 (в першому випадку а=3,5, а другому випадку а=7/3<3, а тому другий випадок нас не влаштовує). Таким чином, при а>3 умова задачі виконується лише, коли а=3,5. Надалі розглядаємо випадок, коли 2≤6/а, що рівносильно а≤3. У цьому випадку умова ax>6 не буде виконуватись для х=2. Отже, в цьому випадку коренем рівняння може бути лише х=3. Для х=3 повинні виконуватись умови 3а>6 та 3а≠7, а тому 2<а≤3 та а≠7/3. Таким чином, остаточно, умова задачі виконується тоді і тільки тоді, коли а є (2; 7/3)U(7/3;3]U{3,5}. Отже, найбільше ціле а дорівнює 3, найбільше дійсне а дорівнює 3,5. Відповідь: 3+3,5=6,5. Щодо останнього рівняння з параметром, то на мою думку, рівняння такого типу навряд чи буде на НМТ, оскільки є складнішим за рівняння з демонстраційного тесту НМТ.





