Тригонометрические формулы: что нужно знать для НМТ по математике и не только

Тригонометрические функции, такие как синус, косинус, тангенс и котангенс, необходимы не только для решения теоретических задач. Ведь они связаны с измерением углов, а этот навык необходим во многих профессиональных областях: архитектуре, искусстве, медицине, автомеханике, исследовании природных явлений, например, преломления света. p>

НМТ содержит значительный пласт задач, основанных на тригонометрии. Поэтому ученики должны уделять особое внимание этому разделу и хорошо усвоить азы — значения тригонометрических функций. Вообще готовиться к тесту по математике лучше при поддержке профессионального репетитора. На BUKI найти такого специалиста можно за несколько минут, применив поисковые фильтры.

Статья полезна для школьников и будущих абитуриентов, готовящихся к НМТ. В ней собран исчерпывающий материал обо всех тригонометрических формулах и функциях, а также их практическом применении для решения задач.

Что такое тригонометрия и почему тригонометрические формулы важны для НМТ?

Такой раздел математики, как тригонометрия, школьники обычно начинают изучать в 10 классе. Знакомство с разделом начинается с темы «Синус, косинус, тангенс, котангенс угла». Собственно, сам раздел исследует соотношение между сторонами и углами треугольников.

Впервые способы решения треугольников были найдены древнегреческими астрономами Гипархом и Клавдием Птолемеем.

Вот какие темы по тригонометрии выносятся на НМТ:

• Определение синуса, косинуса, котангенса числового аргумента
• Основные соотношения между тригонометрическими функциями одного аргумента
• Формулы сведения li>
• Формулы сложения и следствия из них
• Методы решения простейших тригонометрических уравнений
• Тригонометрические функции и их основные свойства

Участник тестирования, согласно стандартам Программы НМТ-2026 по практическим навыкам, должен уметь:

• выполнять тождественные преобразования тригонометрических выражений и находить их числовое значение при заданных значениях переменных li>
• решать простейшие уравнения, содержащие тригонометрические выражения
• решать неравенства, содержащие тригонометрические выражения
• использовать графический метод решения уравнений, неравенств и их систем
• применять уравнения, неравенства и системы уравнений к решению текстовых задач
• строить графики тригонометрических функций
• использовать преобразования графиков функций

Тема тесно связана с такой областью математики, как геометрия. Вычисление углов и легло в основу формул тригонометрии. p>

Основные тригонометрические функции: синус, косинус, тангенс, котангенс

Дадим определение синуса и косинуса через углы прямоугольного треугольника: p>

• Синус в прямоугольном треугольнике синус острого угла определяется как отношение противоположного катета к гипотенузе.
• Косинус — это отношение прилегающего катета к гипотенузе в прямоугольном треугольнике.

Эти соотношения легче представить с помощью рисунка, где α — это острый угол, а — противоположный ему катет треугольника, b — прилегающий к нему катет треугольника, с — гипотенуза треугольника.

Дадим определение еще двум функциям:

• Тангенс — это отношение длины противоположного катета к длине прилегающего катета.
• Котангенс — это отношение длины прилегающего катета к длине противоположного катета.

Рассмотрим их с помощью угла и формул.

p>

Графические материалы взяты с учебной платформы МійКлас.

Таблица тригонометрических функций

Начнем с общих значений.

В таблице дано определение sin и cos через отношение сторон треугольника. А определение tg и ctg представлено как через отношение сторон треугольника, так и через соотношение sin и cos.

Таблица значений тригонометрических функций для углов 0°, 30°, 45°, 60°, 90°

Это база для учеников, которые только начали изучать тригонометрические функции.

Полная таблица тригонометрических функций для углов от 0° до 180° с шагом в 1° содержится на сайте ФинКалк.

Как запомнить таблицу тригонометрических функций быстро и эффективно?

Прежде всего важно использовать наглядные изображения. Так, визуализация углов помогает удержать формулы в памяти значительно дольше, чем зубрежка. Попробуйте понять:

• 30° и 60° – это углы в прямоугольном треугольнике 1–√3–2
• 45° – равнобедренный треугольник со сторонами 1–1–√2

Это, кстати, не единственный способ эффективного запоминания. Вот еще несколько:

1. Техника мнемонических фраз. Подходит для изучения закономерностей. Например, «синус растет с нуля, а косинус падает с единицы».

Еще одна закономерность: таблица синусов и косинусов — зеркальная.

• sin(0°) = 0 ↔ cos(90°) = 0
• sin(30°) = 1/2 ↔ cos(60°) = 1/2
• sin(45°) = √2/2 ↔ cos(45°) = √2/2

Если запомнить sin, то cos можно просто «прочитать в обратном порядке».

1. Используйте квадратичную закономерность. Синусы углов 0°, 30°, 45°, 60°, 90° можно представить простой формулой:

sin(α) = √n/2, где n = 0, 1, 2, 3, 4.

А косинусы — в обратном порядке: cos(α) = √4-n/2.

Это позволяет не учить всю таблицу, а только последовательность чисел 0, 1, 2, 3, 4.

Все тригонометрические формулы, которые нужно знать

Для практической работы над задачами школьникам нужно знать 7 типов формул.

Основные тождества тригонометрии

«Золотым правилом» тригонометрии считается тождество: sin²α + cos²α = 1.

Отсюда следует, что если известно sin α, то cos α можно найти как: cosα = √1 – sin²α.

Например, если sinα = 3/5, то cosα = √1 – (3/5)2 = 4/5.

Тождества для тангенса и котангенса

Эти формулы связывают tg и ctg с sin и cos:

tanα = sinα/cosα, cotα = cosα/sinα.

Отсюда следует, что: tanα ⋅ cotα = 1.

Например, если sin α = 3/5, cos α = 4/5, то tanα = 3/5 : 4/5 = 3/4; cotα = 4/3.

Формулы сложения и разности: sin(a ± b), cos(a ± b), tg(a ± b), ctg(a ± b)

Базовые тригонометрические формулы включают:

• Формулу синуса суммы: sin(a+b) = sina⋅cosb+cosa⋅sinb

• Формулу косинуса суммы: cos(a+b) = cosa⋅cosb−sina⋅sinb

• Формулу синуса разности: sin(a−b) = sina⋅cosb−cosa⋅sinb

Она была выведена из формулы синуса суммы на основе свойства четности функции косинуса и нечеткости функции синуса.

• Формулу косинуса разности: cos(a−b) = cosa⋅cosb+sina⋅sinb strong>

Она была выведена из формулы косинуса суммы на основе свойства четности функции косинуса и нечетной функции синуса.

Формулы суммы и разности для тангенса:

p>

В этих формулах выражено соотношение между тангенсом общей суммы или разности аргументов и тангенсами отдельных аргументов — слагаемых.

При этом для всех тангенсов выполняются условия:

Формулы суммы и разности для котангенса выводятся следующим образом:

Пример практического применения формул. Нужно вычислить выражение cos110°⋅cos20°+sin110°⋅sin20°.

Это выражение напоминает формулу косинуса разности углов: cos(a−b) = cosa⋅cosb+sina⋅sinb. p>

По этой формуле, имеем cos110°⋅cos20°+sin110°⋅sin20° = cos(110°−20°) = 90°.

Следовательно, cos(110°−20°) = cos90°. А cos90° = 0.

Формулы двойного и тройного аргумента

Формулы для двойного угла — это ряд формул, которые помогают выразить тригонометрические функции угла 2x через тригонометрические функции того же угла x. То есть, по сути, эти тригонометрические формулы упрощают решение сложных уравнений и сводят вычисления к базовым формулам, например, синуса суммы.

Формулы тройного угла позволяют найти значение синуса, косинуса и тангенса угла, кратного трем, с использованием значения этих функций для исходного угла.

p>

Формулы понижения степени: sin²a, cos²a, tg²a, ctg²a

Формулы понижения степени (или формулы возведения в квадрат тригонометрических функций) помогают выражать квадраты синуса, косинуса, тангенса и котангенса через функции одинарного угла.

Это очень удобно, когда нужно упростить тригонометрические выражения или интегрировать тригонометрические функции. Их выводят из основного тригонометрического тождества:

cos2a = cos2a−sin2a = 1−2sin2a = 2cos2a−1. p>

Формулы преобразования произведения в сумму и разность

Мы используем формулы суммы и разности углов, чтобы заменить произведения на сумму или разность синусов или косинусов. Это необходимо для упрощения вычислений.

Ключевые формулы для tg и ctg

Как отмечалось выше, тангенс — это отношение синуса к косинусу. При этом значение угла должно подчиняться условию: α ≠ π/2 + πn, n является Z.

Отсюда получаем еще одну формулу: 1 + tg2α = 1/cos2α.

Котангенс — это отношение косинуса к синусу. При этом угол α ≠ π + πn, n является Z.

Имеем еще одну формулу для котангенса: 1 + ctg2α = 1/sin2α.

Например, нужно вычислить выражение (1+ctg2α)sin2α.

Подставим его в формулу: (1+ctg2α)sin2α = 1/sin2α ⋅ sin2α = 1.

Как применять тригонометрические формулы на практике?

Тригонометрические функции помогают понять, как изменяются стороны треугольника, когда мы изменяем его углы. Это позволяет решать различные задачи, такие как измерение расстояний, высот зданий, углов на карте и т. д.

Например, если у нас есть прямоугольный треугольник и мы знаем один угол и длину одной из сторон, то с помощью тригонометрии можно установить длину другой стороны этого треугольника. p>

Рассмотрим на примере значений для физики. Гармонические колебания в природе или технике происходят по законам синуса или косинуса.

• В электромагнитной волне вектор напряженности электрического поля Е и магнитной индукции В изменяются по синусоидальному закону, взаимно перпендикулярны друг другу и направлению распространения волны.
• Еще один пример синусоидальных колебаний — звук. О значении применения радиоволн и говорить нечего. Это основа для телевидения и связи с космическими спутниками.

Наиболее удобным математическим методом для исследования колебательных процессов являются тригонометрические функции. Вот уравнение гармонического колебания, где тригонометрические формулы помогают находить амплитуду, период, фазу движения: x = Asin(ωt+φ).

Кроме этого, в тригонометрии формулы используют для: моделирования движения, создания 3D-графики и анимаций. p>

Также пилоты, моряки и топографы используют синусы и косинусы для расчета направлений, расстояний между точками на сферической поверхности Земли, даже в системах GPS.

Тригонометрические формулы помогают измерять расстояния, углы и высоты, когда это невозможно сделать напрямую. Например, зная угол подъема на гору и расстояние до нее, по формуле h = d⋅tanα можно найти высоту h. Кроме того, при проектировании зданий и мостов вычисляют наклоны, длины перекрытий и угловые соединения.

Формулы тригонометрических уравнений

Тригонометрическое уравнение — это уравнение, в котором неизвестное находится внутри тригонометрической функции: sinx, cosx, tanx, cotx. Например: sinx = 1/2; cos2x = 0; 2sinx – √3 = 0.

Формулы тригонометрических уравнений включают обратные тригонометрические функции.

Для синуса: sin (α) = a, отсюда α = (−1)k arcsin(a) + πk, k ∈ Z.

Или x = arcsina+2πn, x = π−arcsina+2πn.

Для косинуса: cos(β) = a, откуда β = ±arccos(a)+2πn, n ∈ Z.

То есть x = arccosa+2πn; x = −arccosa+2πn.

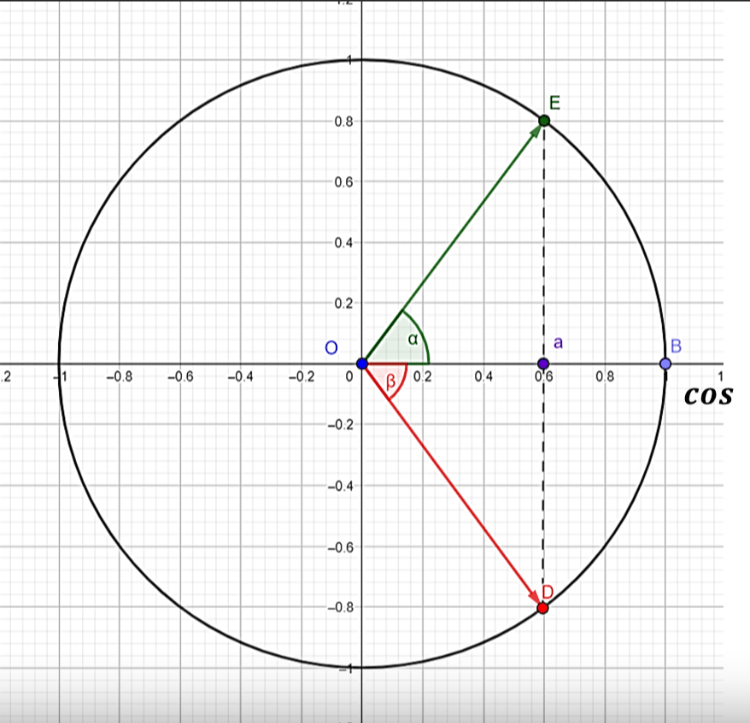
Для тангенса: tgα = b, отсюда α = arctgb+πk, k ∈ Z. p>

Тангенс имеет период π.

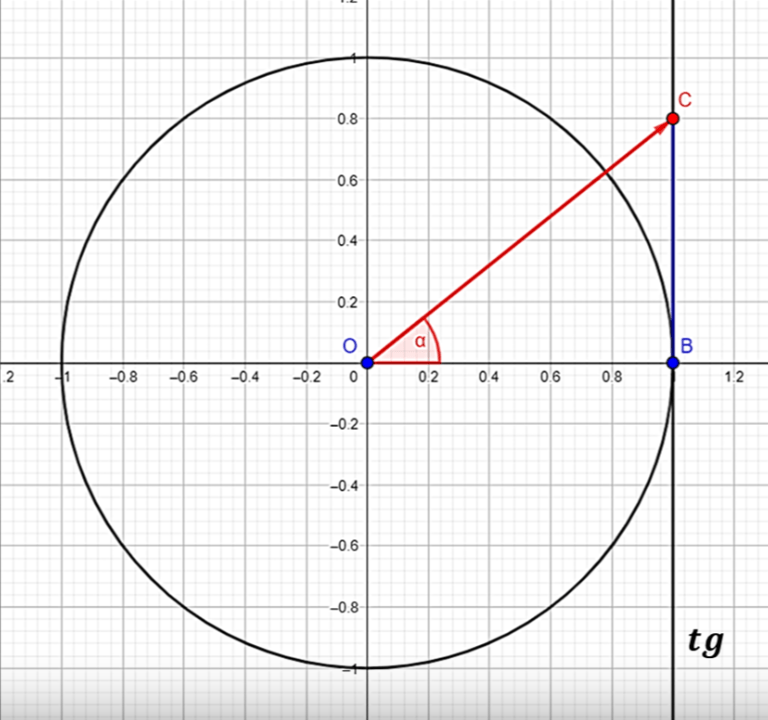
Для котангенса: ctgβ = a, откуда β = arctga+πn, n ∈ Z.

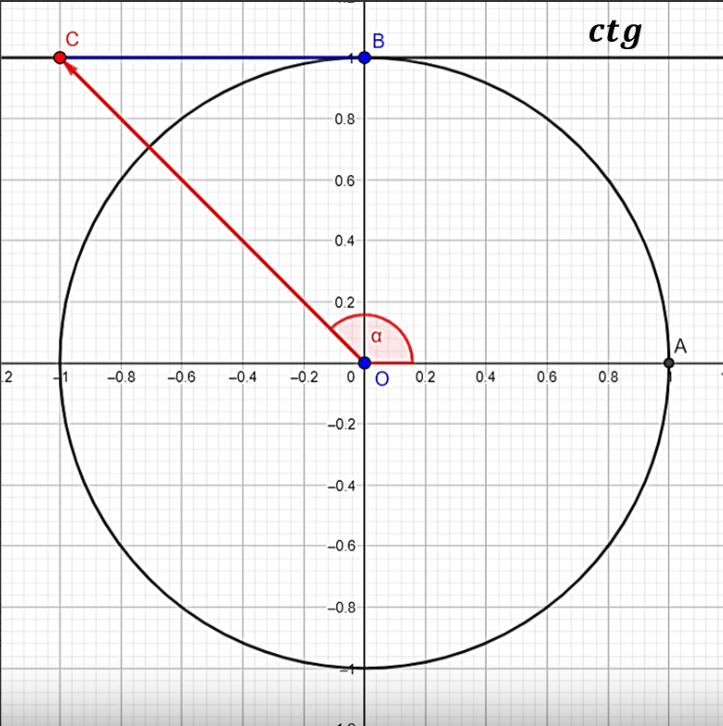
Мы рассмотрели 4 формулы для простейших уравнений.

Обратим также внимание на особенности уравнений, если α = 0, 1, –1.

Сложные тригонометрические уравнения нужно сводить к простым с одной функцией или одним аргументом. Среди других методов решения таких уравнений выделяют разложение на множители, замену переменных, сведение к однородным уравнениям.

Примеры решения типовых тригонометрических уравнений

В этом разделе проанализируем решение уравнений, которые входили в задачи НМТ за 2022–2025 годы.

Уравнение 1: sin4x = –1.

Решение:

sinα = −1.

Это уравнение выполняется тогда, когда угол α равен:

α = 3π/2 + 2πn, n ∈ Z. Ведь синус равен –1 в точке 3π/2 и повторяется через 2π.

Подставляем α = 4x, 4x = 3π/2 + 2πn.

Чтобы найти х, разделим обе части на 4: х = 3π/8 + πn/2, n ∈ Z.

Уравнение 2: cos(3x) = 1/2.

Решение:

Уравнение cos x = a при |а| < 1 имеет решение ±arccos(a)+2πn, n ∈ Z.

Следовательно, 3x = ±arccos1/2 + 2πn, n ∈ Z.

3x = ±π/3 + 2πn, n ∈ Z.

x = ±π/9 + 2πn/3, n ∈ Z.

Уравнение 3: tg(3x) = – 1.

Решение:

3x = arctg (– 1) + sin πn, n ∈ Z.

3x = – π/4 + πn, n ∈ Z.

x = – π/12 + πn/3, n ∈ Z.

Уравнение 4: Определите наименьшее значение а, при котором имеет корни уравнение:

sin x + π/3 = 2a2 + 5a – 6.

Решение:

Данное тригонометрическое уравнение имеет корни, если удовлетворяет условию |2a2 + 5a – 6| ≤ 1.

Нам нужно решить систему неравенств второй степени. p>

Чтобы найти еще два значения а, нужно решить квадратное уравнение.

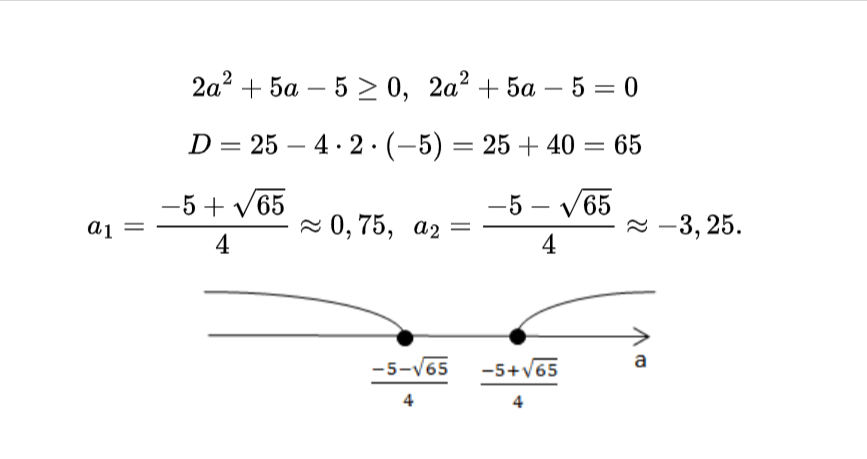
Все решения системы: –3,5; –3,25; 0,57; 1.

Наименьшим значением а является –3,5.

Подготовка к НМТ: как эффективно повторить тригонометрию

Тригонометрические функции могут быть представлены в задачах мультитеста по-разному: p>

• на определение длины стороны треугольника или прямоугольника
• на согласование выражений с утверждениями об их значении
• для упрощения выражений (например, (1 – sin2 α) ⋅ tg2 α))
• для соотнесения функции с ее свойствами
• для тождества тригонометрических выражений
• в составе тригонометрических неравенств и их систем
• на вычисление значения выражения с синусом, если известно значение этого выражения с косинусом и наоборот

Поэтому рекомендуем решать как можно больше таких задач. Для этого можете воспользоваться тренировочными тестами a> на портале osvita.ua образцами тестов за прошлые годы. Работайте с тригонометрической таблицей почти каждый день, решая типовые уравнения.

Чтобы надежно усвоить материал, важно учить не формулы, а взаимосвязи. Вместо того чтобы зубрить, нарисуйте круг единичного радиуса:

• отмечайте углы в градусах и радианах
• помечайте, где sin > 0, где cos < 0
• подписывайте типовые значения (0°, 30°, 45°, 60°, 90°)

Это помогает запомнить все через зрительные образы и не путать знаки в формулах.

А чтобы подготовиться на высшем уровне, лучше найти репетитора по математике для систематических занятий. Педагог, специализирующийся на подготовке к НМТ, сможет объяснить все нюансы тестирования и особенности заданий. Репетитор составит план повторения с учетом текущего уровня знаний и времени, оставшегося до экзамена.

Заключение

Тригонометрия на школьном уровне довольно понятна, если уметь практически применять формулы, запомнить знаки функций в четвертях, повторять таблицу значений для стандартных углов (30°, 45°, 60°).

Блок НМТ по математике может содержать от 1 до 2–3 заданий на синус, косинус, реже — тангенс или котангенс. Составьте план подготовки по тренировочным упражнениям минимум на месяц, выполняйте до 20 практических заданий на вычисление, упрощение выражений, тригонометрические уравнения, нахождение угла по значению функции.

Если тема для ученика сложная и он или она допускает ошибки в 50% заданий, стоит подыскать репетитора для индивидуального объяснения тем.