У зв’язку з тим, що у Європу виїхало багато наших громадян, зокрема, й абітурієнтів, низка європейських університетів пропонують українським учням здобувати вищу освіту у них. Умови навчання можуть бути різними. Деякі університети пропонують повністю безкоштовне навчання для українців, інші – безкоштовне навчання лише протягом першого року навчання, тощо. Окремі університети, як наприклад Краківська Політехніка, «заманюють» наших учнів, навіть, тим, що обіцяють перший рік безкоштовне навчання українською мовою (далі навчання польською чи англійською і платне). Перед тим, як визначитись куди саме вступати, варто детально ознайомитись з умовами (чи повністю безкоштовним буде навчання, чи протягом всього періоду навчання, тощо), а також варто оцінити свої «сили», адже при вступі потрібно буде здавати екзамен. Тому слід поцікавитись по якій програмі готуватись до вступних екзаменів та ознайомитись зі зразками завдань для них. Розглянемо які задачі з математики можуть бути на вступних екзаменах в польських вузах на прикладі офіційно оприлюднених зразків завдань Краківської Політехніки.
Як і в Україні, у Польщі традиційними є задачі з параметрами. Рівняння з 16-ї задачі можна переписати у вигляді (х+а)²+2(х+5)²=0, звідки (х+а)²= –2(х+5)². Оскільки, (х+а)²≥0 та –2(х+5)²≤0, то задане рівняння матиме розв’язки у дійсних числах тоді і тільки тоді, коли (х+а)²=0 та –2(х+5)²=0, звідки х= –а та х= –5. Отже, а=5. Ну, а далі неважко переконатись, що якщо а=5, то задане рівняння має єдиний корінь. Справді, при а=5 рівняння набуває вигляду (х+5)²+2(х+5)²=0, звідки 3(х+5)²=0, звідки х= –5 – єдиний корінь. Можна задане рівняння з параметром розв’язати й іншим (більш звичним для типових українських задач, але більш громіздким) способом. Для цього спочатку наше рівняння перепишемо у вигляді х²+2ах+а²+2х²+20х+50=0, звідки 3х²+(2а+20)х+(а²+50)=0. Тоді дискримінант D=(2а+20)²–4∙3(а²+50)= –8а²+80а–200= –8(а²–10а+25)= –8(а–5)². Для того, щоб задане рівняння мало єдиний розв’язок, необхідно і достатньо, щоб дискримінант дорівнював нулю. Тоді –8(а–5)²=0, звідки а=5.

Функція з 23-ї задачі буде парною, якщо f(–x)=f(x). Матимемо, що f(–x)=(а+2)х²–(5а–4)х+2а. Тоді (а+2)х²+(5а–4)х+2а= (а+2)х²–(5а–4)х+2а, звідки 2(5а–4)х=0. Остання рівність виконуватиметься при довільному дійсному х тоді і тільки тоді, коли 5а–4=0, звідки а=0,8.
Серед краківських задач є чимало алгебраїчних рівнянь.
У четвертій задачі слід почати з ОДЗ: х²>0, х²≠1, х+2>0. Нерівність х²>0 рівносильна нерівності х≠0. Своєю чергою, із х²≠1 випливає, що х≠ ±1, а із х+2>0 – що х> –2. Тоді ОДЗ: х є (–2; –1) U (–1; 0) U (0; 1) U (1; +∞). Тоді отримаємо, що х+2=х². Це квадратне рівняння має два корені: х= –1 та х=2. Однак, корінь х= –1 не задовольняє ОДЗ. Тому задане рівняння має єдиний корінь х=2.
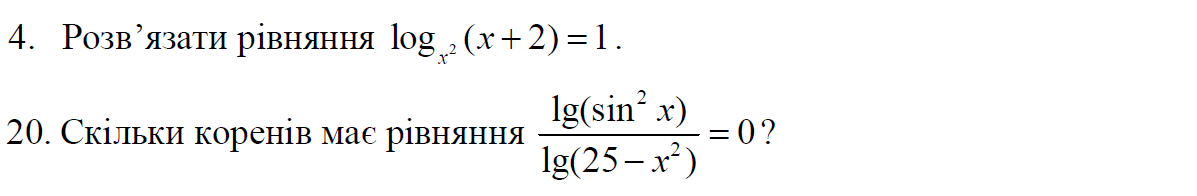
З ОДЗ слід почати і в 20-тій задачі: sin²x>0 та 25–х²>0 та lg(25–х²)≠0. Нерівність sin²x>0 рівносильна нерівності sinx≠0, а тому х≠πk, k є Z. Нерівність 25–х²>0 слід переписати у вигляді (5–х)(5+х)>0, звідки неважко встановити, що х є (–5; 5). Враховуючи те, що х≠πk, k є Z та те, що х є (–5; 5), матимемо, що на проміжку (–5; 5) змінна х не може набувати значень –π, 0 та π. Оскільки, lg(25–х²)≠0, то 25–х²≠1, звідки х²≠24, звідки х≠ ±√̅2̅4̅ . Остаточно ОДЗ: х є (–5; –√̅2̅4̅ ) U (–√̅2̅4̅ ; –π) U (–π; 0) U (0; π) U (π; √̅2̅4̅ ) U (√̅2̅4̅ ; 5). Розв’язуємо рівняння lg(sin²x)=0, звідки sin²x=1, звідки х=0,5π+πk, k є Z. Враховуючи ОДЗ, отримаємо, що наше рівняння має чотири корені: х₁= –1,5π, х₂= –0,5π, х₃=0,5π та х₄=1,5π.
Однак не варто лякатись, бо серед краківських екзаменаційних задач є й багато значно простіших задач, наприклад, такі:






