
Визначення і способи знаходження середнього арифметичного, учні вивчають у 5 класі, але це важливо знати й під час складання іспитів у старших класах. Тому пропонуємо вивчити або поновити в пам’яті важливі знання, потренуватися розв’язувати задачі на середнє арифметичне для 5 класу та більш складні, які можуть трапитися на ЗНО.
Що таке середнє арифметичне?
У школі та буденному житті часто вживаються словосполучення «середня зарплата», «середня оцінка», «середній вік». Основою для всіх цих понять є математичний термін середнє арифметичне.
Середнім арифметичним кількох чисел називається частка від ділення суми цих чисел на їхню кількість. Тобто, щоб його знайти, потрібно суму чисел поділити на їхню кількість.
Формула середнього арифметичного двох чисел виглядає так:
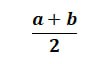
Як знайти середнє арифметичне?
Визначення середнього арифметичного звучить страшно й незрозуміло, але насправді для його знаходження виконується лише дві арифметичні дії – додавання і ділення. Наприклад, учень бере три якісь числа, додає їх і ділить на 3. Відповідь і буде середнім арифметичним.
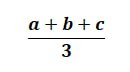
Розглянемо приклад. Вам необхідно знайти середнє арифметичне чисел 7 і 3. Перший крок – ви їх додаєте й отримаєте 10. Далі цю суму потрібно поділити на 2, тобто на кількість чисел.
- 7 + 3 = 10.
- 10 : 2 = 5.
Відповідь другої дії і є середнім арифметичним.
Розглянемо ще один приклад, який близький усім школярам. Учня наприкінці чверті цікавить питання, яка оцінка в нього буде з певного предмета. Для отримання відповіді, необхідно вирахувати середній бал.
Наприклад, учень отримав за чверть такі бали: 5, 4, 5, 3, 3, 5, 4, 5, 4, 5. Щоби порахувати середній бал, потрібно скласти всі оцінки, а потім розділити на їх кількість (10).
- 5 + 4 + 5 + 3 + 3 + 5 + 4 + 5 + 4 + 5 = 43
- 43 : 10 = 4,3
Відповідь: 4,3 – середнє арифметичне.
Читайте також: Збираємо шкільний рюкзак: поради та чекліст

Задачі на середнє арифметичне для 5 класу
Коли учень зрозумів, як знайти середнє арифметичне, йому важливо навчитися розв’язувати задачі із цієї теми, у яких не все так просто. Як і в будь-яких математичних задачах, потрібно:
- Уважно вивчити умову і зробити короткий запис, у якому позначені всі взаємозв’язки між числами;
- Декілька разів прочитати питання, щоб точно розуміти, що саме необхідно знайти.
Часто трапляється ситуація, що школяр знає формулу знаходження середнього арифметичного, але через неуважність додає не ті числа або враховує зайві показники й помиляється в обчисленнях.
Розглянемо цікаві задачі на середнє арифметичне, які учні розв’язують у 5 класі.
Задача № 1
Діти працювали в саду і збирали груші. Артем зірвав 2 груші, Емілія – 4, Вова – 6. Малеча склала їх у корзину і віднесла додому. Мама поділила груші порівну між малюками. Скільки груш отримала кожна дитина?
Щоб розв’язати задачу, необхідно знайти середнє арифметичне трьох чисел.
2 + 4 + 6 = 12 груш (разом зібрали діти)
Коли учень знає, скільки фруктів знайдено всього, необхідно цю суму розділити на кількість дітей.
12 : 3 = 4 груші (отримала кожна дитина)
Відповідь: 4.
Задача № 2
Упродовж вивчення теми учень здобув за усні відповіді 7 і 12 балів, написав дві самостійні роботи на 8 і 9 балів, а контрольну – на 9. Якою буде його тематична оцінка?
Тематична оцінка є близькою до середнього балу за всі види робіт. Щоб дати відповідь на головне питання задачі, необхідно спочатку знайти середнє арифметичне всіх оцінок. Для цього додаємо всі здобуті бали.
7 + 12 + 8 + 9 + 9 = 44
Далі загальну кількість балів потрібно поділити на кількість оцінок, тобто на 5.
44 : 5 = 8,8
8,8 – це середнє арифметичне, але такої оцінки немає, тому вчитель округлить це число до 9.
Відповідь: 9 балів – тематична оцінка учня.
Задача № 3
Середнє арифметичне 4 чисел дорівнює 3,4, а середнє арифметичне інших 6 чисел – 8,3. Знайдіть середнє арифметичне всіх 10 чисел.
У подібних задачах учні часто помиляються і знаходять середнє арифметичне двох чисел – 3,4 і 8,3. Але важливо врахувати, що тут не 2 числа, а 10. Тому щоб знайти середнє арифметичне 10 чисел, потрібно дізнатися суму цих 10 чисел.
Спочатку знаходимо суму 4 чисел. Для цього середнє арифметичне необхідно помножити на кількість чисел.
3,4 * 4 = 13,6
Тепер аналогічно рахуємо суму 6 чисел.
8,3 * 6 = 49,8
Наступним кроком буде знаходження суми 10 чисел.
13,6 + 49,8 = 63,4
Залишилося знайти середнє арифметичне чисел.
63,4 : 10 = 6,34
Відповідь: 6,34 – середнє арифметичне 10 чисел.
Задача № 4
Середній вік гравців футбольної команди, які брали участь у грі – 22 роки. Після того, як за порушення з поля був вилучений гравець, середній вік футболістів, що залишилися в грі, становив 21 рік. Скільки років було гравцеві, якого вилучили з поля?
Спочатку учень має знайти суму років усіх гравців, які брали участь у грі з першої хвилини. Для цього потрібно пригадати, шо футбольна команда – це 11 людей.
22 * 11 = 242 (р)
Тепер необхідно знайти суму років гравців, які залишилися на полі після вилучення одного гравця, тобто 10 людей.
21 * 10 = 210 (р)
На останньому етапі учень знаходить різницю двох середніх арифметичних і дізнається вік футболіста, який порушив правила й був дискваліфікований.
242 — 210 = 32 (р)
Відповідь: 32 роки.
Задача № 5
Фермер зібрав із кожного гектара поля, загальна площа якого 30 гектарів, 30,2 Ц пшениці, а з кожного гектара поля, площею 20 гектарів, по 32,3 Ц пшениці. Який середній урожай з одного гектара зібрав фермер?
Щоб не заплутатися в даних, учневі важливо робити схематичний запис умови.
30 га – 30,2 ц з 1 га
20 га – 32,3 ц з 1 га
Необхідно знайти весь урожай з обох полів.
- 30 * 30, 2 = 906 (ц) зібрали з поля, площею 30 га.
- 20 * 32,3 = 646 (ц) зібрали з поля, площею 20 га.
- 906 + 646 = 1522 (ц) зібрали з двох полів.
Тепер учень має визначити загальну площу полів і поділити на неї весь врожай.
- 30 + 20 = 50 (га) площа двох полів.
- 1522 : 50 = 31,04 (ц)
Відповідь: 31,04 ц – середній урожай пшениці з одного гектара поля.
Задача № 6
Автомобіль їхав 3,4 години по шосе зі швидкістю 90 км/год і 1,6 години грунтовою дорогоюі. З якою швидкістю їхав автомобіль грунтовою дорогою, якщо середня швидкість на всьому шляху становила 75,6 км/год.
У цій задачі середня швидкість відома й потрібно знайти швидкість на одній частині шляху, тобто це є обернена задача на середню швидкість.
3,4 год – 90 км/год
1,6 год – х км/год
сер. шв. – 75,6 км/год
Складаємо рівняння на основі формули середнього арифметичного і спрощуємо його.
(3,4 * 90 + 1,6х): (3,4 + 1,6) = 75,6
(306 + 1,6х): 5 = 75,6
306 + 1,6х = 378
1,6х = 378 - 306
1,6х = 72
х = 72: 1,6
х = 45
Відповідь: 45 км/год – швидкість, з якою автомобіль рухався грунтовою дорогою.
Щоб навчитися правильно і швидко розв’язувати задачі із цієї теми, школяреві важливо багато практикуватися та мати якісні знання з інших тем математики. Коли дитина погано засвоїла ділення, вона не зможе знайти середнє арифметичне чисел. А погане розуміння середнього арифметичного не дасть змоги розв’язувати задачі на середню швидкість.
Якщо школяр має проблеми з дисципліною, важливо вчасно звернутися по допомогу до репетитора з математики. Бо незрозумілі теми будуть накопичуватись як сніжний ком, а успішність у школі й мотивація до навчання будуть знижуватися.
Педагог проведе тестування, у якому виявить прогалини в знаннях, поспілкується з учнем і дізнається про його проблеми та мету вивчення математики, на основі отриманої інформації складе індивідуальний план навчання.
На уроках викладач орієнтується лише на одного учня і проводить заняття в комфортному для нього темпі, приділяє необхідний час кожному питанню. Знайти репетитора з математики для поточних уроків чи підготовки до ЗНО ви можете на сайті BUKI.
Читайте також: Властивості і формули логарифмів

Середнє арифметичне: підготовка до ЗНО
У завданнях основної сесії ЗНО може трапитися задача на знаходження середнього арифметичного. Тому під час підготовки важливо повторити цю тему й розглянути приклади завдань минулих років.
Ось завдання № 12 зі ЗНО з математики 2018 року.
Учень із понеділка до п’ятниці записував час у хвилинах, який він витрачав на дорогу до школи та зі школи.
|
Понеділок |
Вівторок |
Середа |
Четвер |
П’ятниця |
|
|
До школи |
19 |
20 |
21 |
17 |
23 |
|
Зі школи |
28 |
22 |
20 |
25 |
30 |
Необхідно знайти, на скільки хвилин у середньому дорога зі школи була триваліша від дороги до школи. Щоб відповісти на питання, необхідно спочатку знайти середній час дороги до школи й середній час дороги зі школи.
Для знаходження середнього часу подолання шляху до школи додаємо всі хвилини й ділимо на кількість днів.
(19 + 20 + 21 + 17 + 23) : 5 = 100 : 5 = 20 (хв) у середньому тривала дорога до школи.
Середній час дороги зі школи рахуємо аналогічно.
(28 + 22 + 20 + 25 + 30) : 5 = 125 : 5 = 25 (хв) у середньому тривала дорога зі школи.
Тепер потрібно знайти різницю цих середніх часів.
25 - 20 = 5 (хв)
Відповідь: Дорога зі школи в середньому тривала на 5 хвилин довше дороги до школи.
Щоб якісно підготуватися до ЗНО, важливо системно займатися і мати можливість отримати пояснення всіх незрозумілих тем від досвідченого викладача. Знайти репетитора з математики чи іншої дисципліни ви можете на сайті BUKI.
Читайте також: Геометрична прогресія: пояснення та формули
Сподобалась стаття? Оцініть
2.93
На основі відгуків 14 користувачів





