Метод раціоналізації
Напевно, більшість читачів уже стикалась з логарифмічними нерівностями. Що у них відзнакового? Перше, що приходить на думку, — це можлива зміна знаку залежно від значення основи. Нагадаю, що у загальному випадку можливі такі випадки:
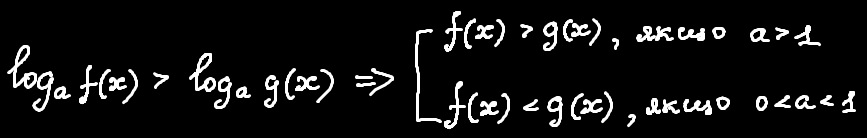
Проте що робити у такому випадку logf(x)g(x) > h(x)? Про це ми і поговоримо сьогодні.
Розглядати ми будемо такий приклад: 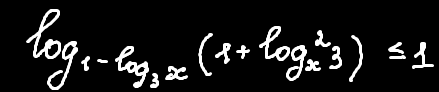
Я наведу декілька методів розв'язання, щоб показати альтернативні варіанти та обґрунтувати свою суб'єктивну думку щодо переваг методу раціоналізації.
Перш ніж почати, запишемо ОДЗ для цієї нерівності, щоб використовувати її для всіх методів нижче. Нагадаю, что аргумент логарифма має бути додатнім, а його основа — більша за нуль і не дорівнювати одиниці. У нас 2 основи та 1 аргумент "зовнішнього" логарифма ("трійку" нема сенсу розглядати, бо вона завджи додатня). Запишемо умови:
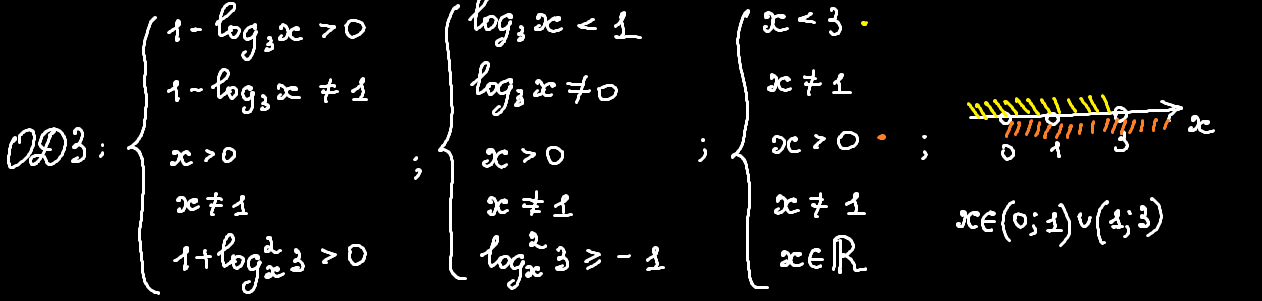
Отже, нашу нерівність визначено при xє(0;1)∪(1;3). Приступімо до розв'язання!
1 метод: роздивитись всі можливі випадки
На мою думку, це перше, що спадає на розум. Згідно з тим, що знак логарифмічної нерівності залежить від основи, то чому б не роздивитись ті 2 випадки окремо для основ?
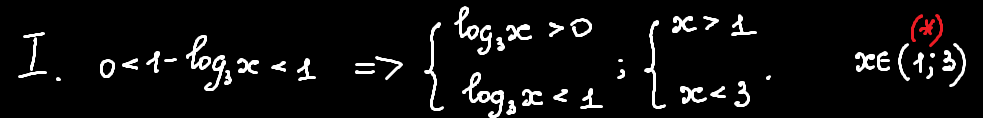
Отже, для такого проміжку основа буде від 0 до 1, а це означає, що знак нерівності буде змінюватись. Далі, взявши до уваги проміжок, для якого це виконується (виділено червоною зірочкою), розв'язуємо нерівність:
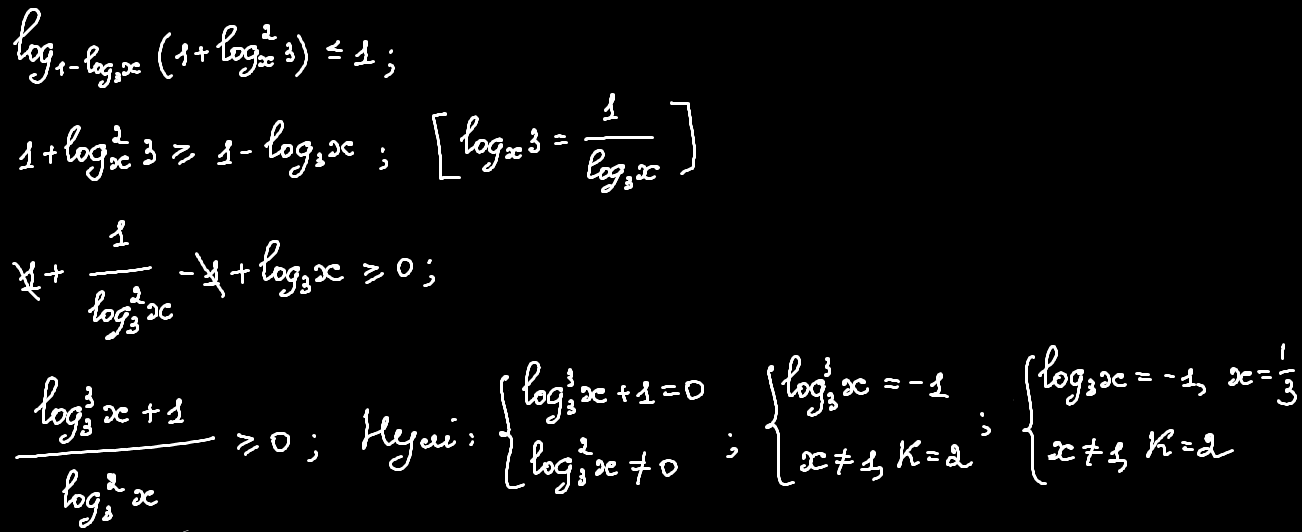
Окрім формули зміни основи та аргумента логарифма (зазначено у квадратних дужках зверху), нічого більше застосовано не було. Фінальну нерівність розв'язуємо методом інтервалів: знак на крайньому правому "+", інші — чергуються.
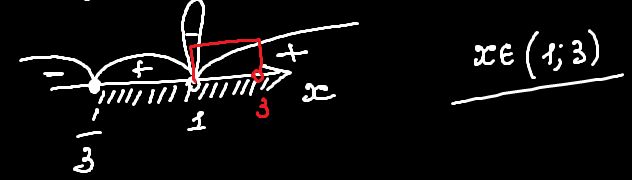
Червоним зображено проміжок, для якого виконується потрібна умова, а біла штриховка показує усі значення змінної, які задовільняють нерівності. Пелюстка з'являється тому, що х = 1 — корінь другої кратності, а це означає, що на знак він впливати не буде (тому нема і чергування). Отже, для цього кроку відповідь: xє(1; 3).
Переходимо до другого випадку (основа більша за одиницю). Всі інші дії — аналогічні.
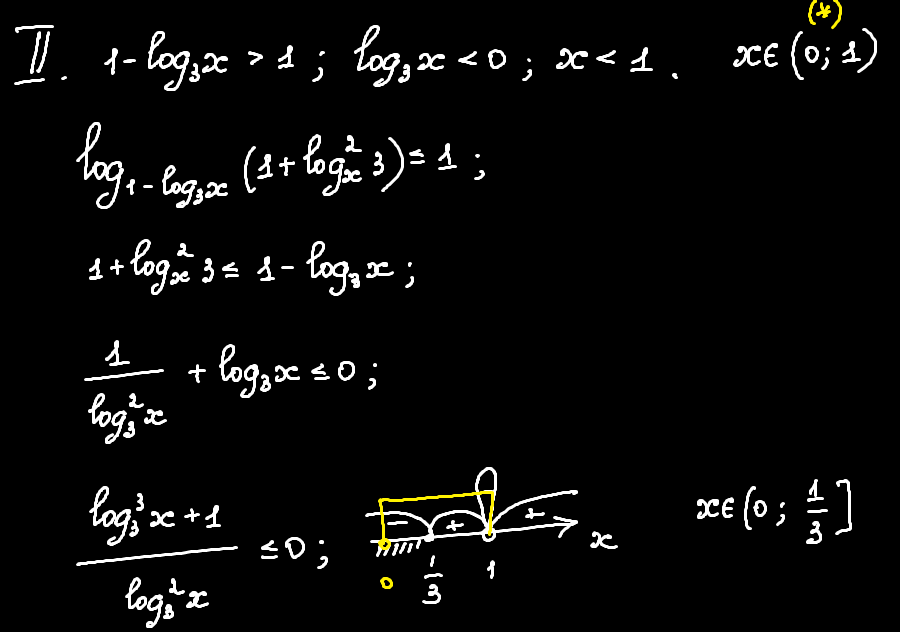
Жовта умова зображено прямокутними дужками, розв'язок нерівності — білою штриховкою. Отже, розв'язком для цього випадку буде проміжок: xє(0;1/3].
Об'єднуючи ці 2 розв'язки, остаточна відповідь: xє(0;1/3]∪(1;3).
Це був, мабуть, найочевиднійший метод, але, на жаль, найоб'ємніший. Рухаємось далі до інших!
2 метод: перехід до постійної основи
Давайте сформулюємо таке твердження у голові: якщо труднощі виникають через "непостійність" основи, то чому б не змінити її на якусь константу, про яку завджи відомо?
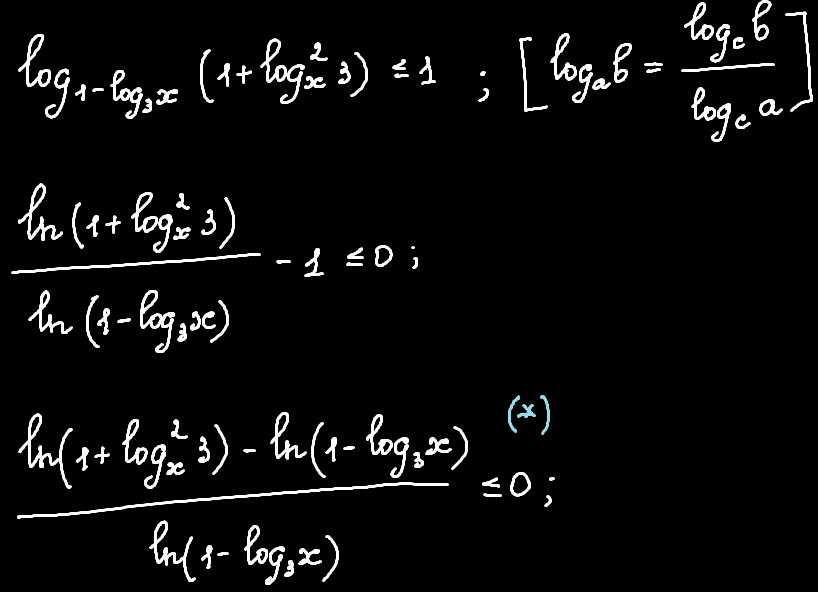
Далі розв'язуємо стандартним методом інтервалів, проте не поспішаємо ставити знаки (це принципово)!
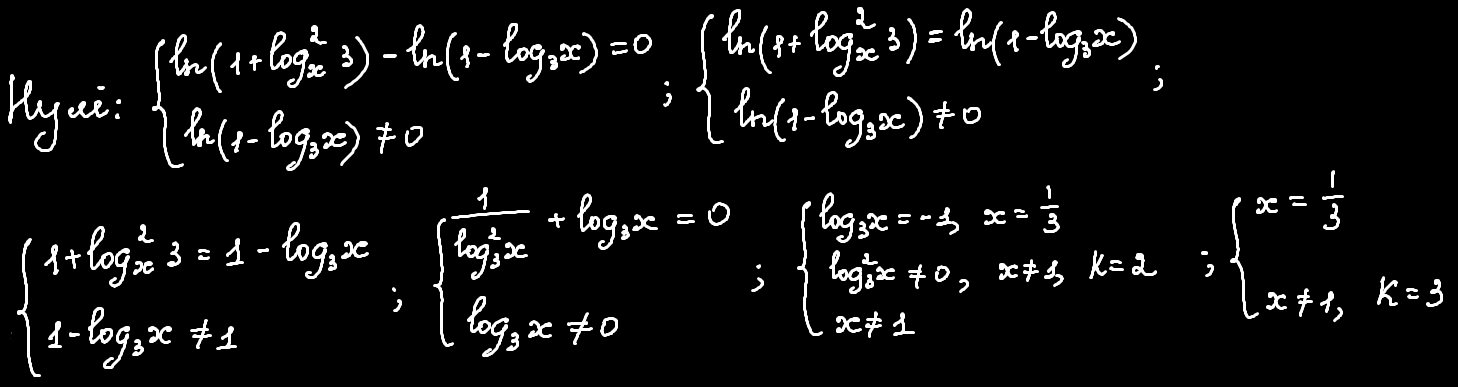
Справа в тому, що ми не можемо однозначно визначити, який знак буде на крайньому правому проміжку (тому що не зрозуміло, що брати за точку опору). У стандартному правилі про визначення знаку на крайньому правому проміжку сказано, що треба дивитись на "мінуси перед іксами", проте.... чи очевидно, куди дивитись тут?
Власне, це один-єдиний, але величезний недолік цього методу — знак треба визначати "методом пробної точки". Недарма я позначив нашу нерівність блакитною зірочкою . Візьмемо будь-яке число з нашого крайнього правого проміжку, наприклад, х = 2, і підставимо його у нерівність:
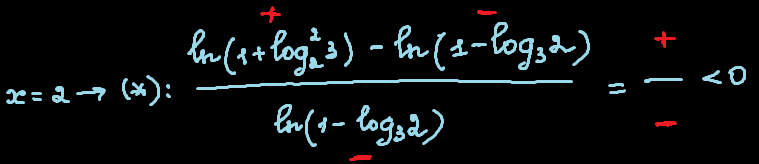
Зі знаками може бути трішечки незрозуміло, тому прикріплю невеличке пояснення:
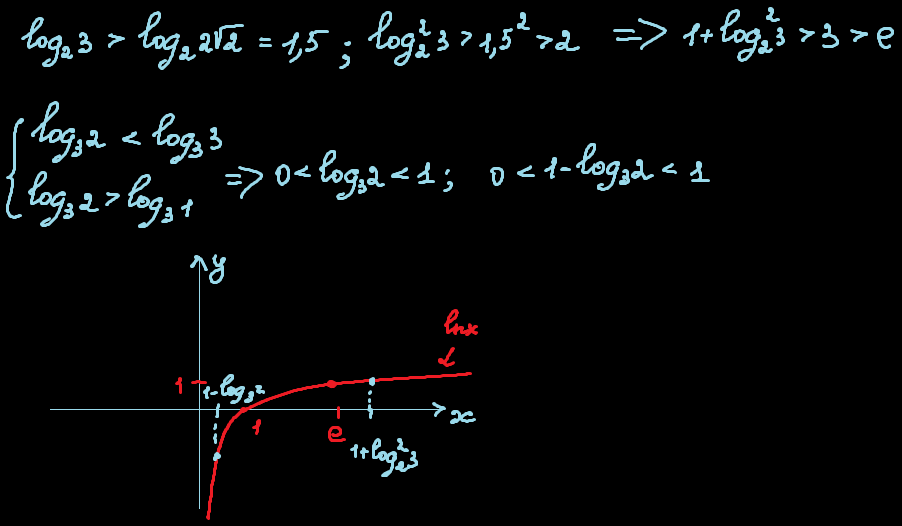
Отримавши, що на крайньому правому знак "мінус", а усі нулі непарної кратності, знаки можна сміливо чергувати:
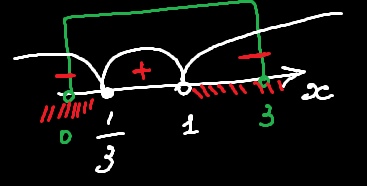
Зелені квадратні дужки — ОДЗ, червона штриховка — розв'язок нерівності. Отже, відповідь: xє(0;1/3]∪(1;3), що співпадає з минулим варіантом розв'язку. На мій смак, через плутанину зі знаками, перший метод навіть краще, але це справа кожного :)
3 метод: метод раціоналізації
Зразу хочу відмітити, що "раціоналізувати", тобто привести до 100% многочленного вигляду, у нас не вийде, бо аргументом логарифма також виступає логарифм. До речі, у цьому і полягає суть методу — перейти від функцій до звичайних многочленів. Сьогодні розглянемо лише формули для логарифмів:
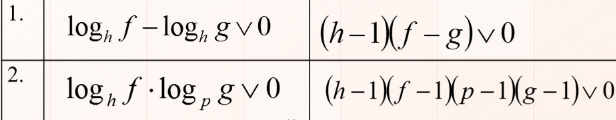
У чому сенс? У першій формулі ми віднімаємо від основи одиницю (це замість розглядання двох випадків, як у першому пункті), а наступним множником є різниця аргументів, яка покаже, умовно, який з логаріфмів більше. Наприклад, якщо основа більше нуля і аргумент першого логарифма більше за аргумент другого, тоді отримаємо "плюс" і "плюс" — і дійсно, зростаючий логарифм буде більше при більшому аргументі.
У другій формулі від аргументів віднімається одиничка, бо loga1 = 0, тобто це нульова точка логарифму.
Сьогодні ми працюватимемо лише з першою формулою. Для початку, перенесемо усе в один бік:
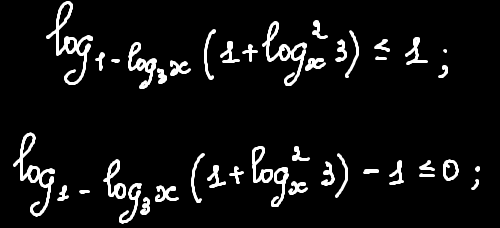
Що робити далі? Далі уявімо одиницю як логарифм, щоб привести наш вираз до того, що наведено у формулі вище:
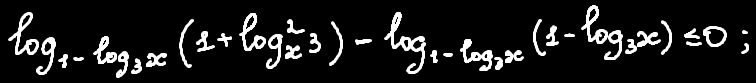
А далі застосовуємо формулу заміни множників (або раціоналізації виразів) і розв'язуємо простеньку нерівність:
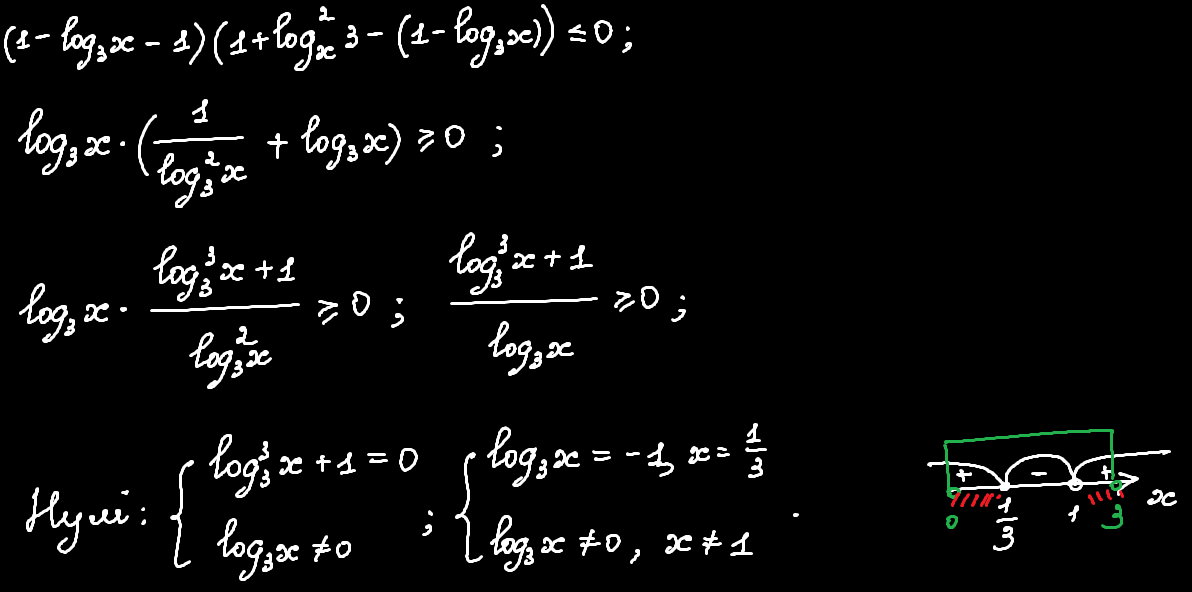
Тут все, як у звичайному методі інтервалів: визначаємо нулі, знаки від крайього право чергуються, причому тут немає проблем із визначенням знаку, як у другому методі; а далі поєднуємо розв'язок (червона штриховка) з ОДЗ (зелена дужка).
Втретє отримуємо відповідь:xє(0;1/3]∪(1;3).
Висновки:
Хочу сказати, що кожен з трьох наведених методів має свою логіку, свої плюси та мінуси. Особисто я віддаю перевагу третьому, бо, по-перше, він дозволяє розв'язати нерівність найбільш компактно, а по-друге, не треба зайвий раз замислюватись щодо можливих підводних каменях зі знаками у методі інтервалів. Загалом, якщо часу достатньо, то на контрольній роботі можна розв'язати якимось двома, щоб на всі 100% бути впевненим у правильності своєї відповіді :)





