Определение и способы нахождения среднего арифметического учащиеся изучают в 5 классе, но это важно и во время сдачи экзаменов в старших классах. Поэтому предлагаем выучить или повторить важные знания, потренироваться решать задачи на среднее арифметическое для 5 класса и более сложные, которые могут встретиться на ВНО.
Что такое среднее арифметическое?
В школе и повседневной жизни часто употребляются словосочетания «средняя зарплата», «средняя оценка», «средний возраст» Основой для всех этих понятий есть математический термин среднее арифметическое.
Средним арифметическим нескольких чисел называется доля от деления суммы этих чисел на их количество. То есть, чтобы его найти, нужно сумму чисел поделить на их количество.
Формула среднего арифметического двух чисел выглядит так:
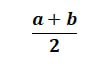
Читайте также: Свойства и формулы логарифмов
Как найти среднее арифметическое?
Определение среднего арифметического звучит страшно и непонятно, но на самом деле для его нахождения выполняется только два арифметических действия – сложение и деление. Например, ученик берет три каких-то числа, добавляет их и делит на 3. Ответ и будет средним арифметическим.
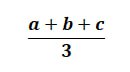
Рассмотрим пример. Вам необходимо найти среднее арифметическое чисел 7 и 3. Первый шаг – вы их добавляете и получаете 10. Далее эту сумму нужно разделить на 2, то есть на количество чисел.
- 7 + 3 = 10.
- 10 : 2 = 5.
Ответ второго действия и является средним арифметическим.
Рассмотрим еще один пример, который близок всем школьникам. Учащегося в конце четверти интересует вопрос, какая оценка у него будет по определенному предмету. Для получения ответа необходимо посчитать средний балл.
Например, ученик получил за четверть следующие баллы: 5, 4, 5, 3, 3, 5, 4, 5, 4, 5. Чтобы посчитать средний балл, нужно сложить все оценки, а затем разделить на их количество (10).
- 5 + 4 + 5 + 3 + 3 + 5 + 4 + 5 + 4 + 5 = 43
- 43 : 10 = 4,3
Ответ: 4,3 – среднее арифметическое.
Читайте также: Собираем школьный рюкзак: советы и чеклист
Задачи на среднее арифметическое для 5 класса
Когда ученик понял, как найти среднее арифметическое, ему важно научиться решать. задачи по этой теме, в каких не все так просто. Как и в любых математических задачах, нужно:
- Внимательно изучить условие и сделать краткую запись, в которой обозначить все взаимосвязи между числами;
- Несколько раз прочесть вопрос, чтобы точно понимать, что именно необходимо найти.
Часто случается ситуация, что школьник знает формулу нахождения среднего арифметического, но по невнимательности добавляет не те числа или учитывает лишние показатели и допускает ошибку в вычислениях.
Рассмотрим интересные задачи на среднее арифметическое, которые учащиеся решают в 5 классе.
Задача № 1
Дети работали в саду и собирали груши. Артем сорвал 2 груши, Эмилия – 4, Вова – 6. Они сложили их в корзину и отнесли домой. Мама поделила груши поровну между малышами. Сколько груш получил каждый ребенок?
Чтобы решить задачу, необходимо найти среднее арифметическое трех чисел.
2+4+6=12 груш (всего собрали дети)
Когда ученик знает, сколько фруктов найдено всего, необходимо эту сумму разделить на количество детей.
12:3 = 4 груши (получил каждый ребенок)
Ответ: 4.
Задача № 2
Во время изучения темы учащийся получил за устные ответы 7 и 12 баллов, написал две самостоятельные работы на 8 и 9 баллов, а контрольную – на 9. Какой будет его тематическая оценка?
Тематическая оценка близка к среднему баллу за все виды работ. Чтобы дать ответ на главный вопрос задачи, необходимо сначала найти среднее арифметическое всех оценок. Для этого добавляем все полученные баллы.
7 + 12 + 8 + 9 + 9 = 44
Дальше общее количество баллов нужно разделить на количество оценок, то есть на 5.
44 : 5 = 8,8
8,8 – это среднее арифметическое, но такового оценки не существует, поэтому учитель округлит это число до 9.
Ответ: 9 баллов – тематическая оценка ученика.
Задача № 3
Среднее арифметическое 4 чисел равно 3,4, а среднее арифметическое остальных 6 чисел – 8,3. Найдите среднее арифметическое всех 10 чисел.
В подобных задачах учащиеся часто ошибаются и находят среднее арифметическое двух чисел – 3,4 и 8,3. Но важно учесть, что здесь не 2 числа, а 10. Поэтому, чтобы найти среднее арифметическое 10 чисел, нужно узнать сумму этих 10 чисел.
Сначала находим сумму 4 чисел. Для этого среднее арифметическое необходимо умножить на количество чисел.
3,4 * 4 = 13,6
Теперь аналогично считаем сумму 6 чисел.
8,3 * 6 = 49,8
Следующим шагом будет нахождение суммы 10 чисел.
13,6 + 49,8 = 63,4
Осталось найти среднее арифметическое чисел.
63,4 : 10 = 6,34
Ответ: 6,34 – среднее арифметическое 10 чисел.
Задача № 4
Средний возраст игроков футбольной команды, участвовавших в игре – 22 года. После того, как за нарушение с поля был удален игрок, средний возраст оставшихся футболистов составил 21 год. Сколько лет было игроку, которого выгнали с поля?
Сначала ученик должен найти сумму лет всех игроков, участвовавших в игре с первой минуты. Для этого нужно вспомнить, что футбольная команда – это 11 человек.
22*11 = 242(л)
Теперь необходимо найти сумму лет игроков, оставшихся на поле после удаления одного игрока, то есть 10 человек.
21*10 = 210(л)
На последнем этапе ученик находит разницу двух средних арифметических и узнает возраст футболиста, нарушившего правила и дисквалифицированного.
242 - 210 = 32 (л)
Ответ: 32 года.
Задача№ 5
Фермер собрал с каждого гектара поля, общая площадь которого 30 гектаров, 30,2 тонн пшеницы, а с каждого гектара поля, площадью 20 гектаров, 32,3 тонн пшеницы. Какой средний урожай с одного гектара собрал фермер?
Чтобы не запутаться в данных, учащемуся важно сделать схематическую запись условия.
30 га – 30,2 тонн с 1 га
20 га – 32,3 тонн с 1 га
Необходимо найти весь урожай с обоих полей.
- 30*30,2 = 906(т) собрали с поля, площадью 30 га.
- 20*32,3=646(т) собрали с поля, площадью 20 га.
- 906+646=1522(т) собрали из двух полей.
Теперь ученик должен определить общую площадь полей и разделить на нее весь урожай.
- 30 + 20 = 50 (га) площадь двух полей.
- 1522 : 50 = 31,04 (т)
Ответ: 31,04 тонн – средний урожай пшеницы с одного гектара поля.
Задача № 6
Автомобиль ехал 3,4 часа по шоссе со скоростью 90 км/ч и 1,6 часа по грунтовой дороге. С какой скоростью ехал автомобиль по грунтовой дороге, если средняя скорость на всем пути составляла 75,6 км/ч.
В этой задачи средняя скорость известна и нужно найти скорость на одной части пути, то есть это обратная задача на среднюю скорость.
3,4 год – 90 км/час
1,6 год – х км/час
средн. скор. – 75,6 км/час
Составляем уравнение на основе формулы среднего арифметического и упрощаем его.
(3,4 * 90 + 1,6ч): (3,4 + 1,6) = 75,6
(306 + 1,6 ч): 5 = 75,6
306 + 1,6 ч = 378
1,6ч = 378 - 306
1,6 ч = 72
х = 72:1,6
х = 45
Ответ: 45 км/ч – скорость, с которой автомобиль двигался по грунтовой дороге.
Чтобы научиться правильно и быстро решать задачи с этой темы, школьнику важно много практиковаться и иметь качественные знания по другим темам математики. Когда ребенок плохо усвоил деление, он не сможет найти среднее арифметическое чисел. А плохое понимание среднего арифметического не позволит решать задачи на среднюю скорость.
Если у школьника проблемы с дисциплиной, важно вовремя обратиться за помощью к репетитору по математике. Непонятные темы будут накапливаться как снежный ком, а успеваемость в школе и мотивация к обучению будут снижаться.
Педагог проведет тестирование, в котором обнаружит пробелы в знаниях, пообщается с учеником и узнает о его проблемах и целях изучения математики, на основе полученной информации составит индивидуальный план обучения.
На уроках преподаватель ориентируется только на одного ученика и проводит занятие в комфортном для него темпе, уделяя необходимое время каждому вопросу. Найти репетитора по математике для текущих уроков или подготовки к ВНО вы можете на сайте BUKI.
Среднее арифметическое: подготовка к ЗНО
В задачах основной сессии ВНО может встретиться задача на нахождение среднего арифметического. Поэтому при подготовке важно повторить эту тему и рассматреть примеры подобных задач прошлых лет.
Вот задание № 12 с ЗНО по математике 2018 года.
Ученик с понедельника до пятницы записывал время в минутах, которое он тратил на дорогу в школу и из школы.
|
Понедельник |
Вторник |
Среда |
Четверг |
Пятница |
|
|
В школу |
19 |
20 |
21 |
17 |
23 |
|
Из школы |
28 |
22 |
20 |
25 |
30 |
Необходимо найти, на сколько минут в среднем дорога из школы была длиннее дороги к школе. Чтобы ответить на вопрос, необходимо сначала найти среднее время дороги в школу и среднее время на дорогу из школы.
Для нахождения среднего времени преодоления пути в школу добавляем все минуты и и делим на количество дней.
(19 + 20 + 21 + 17 + 23): 5 = 100 : 5 = 20 (мин) в среднем длилась дорога в школу.
Среднее время дороги из школы считаем аналогично.
(28 + 22 + 20 + 25 + 30): 5 = 125 : 5 = 25 (мин) в среднем длилась дорога из школы.
Теперь нужно найти разницу этих средних времен.
25 – 20 = 5 (мин)
Ответ: Дорога из школы в среднем длилась на 5 минут дольше дороги в школу.
Чтобы качественно подготовиться к ВНО, важно системно заниматься и иметь возможность получить объяснение всех непонятных тем от опытного преподавателя. Найти репетитора по математике или другой дисциплине вы можете на сайте BUKI.
