Ученикам может показаться, что изучение геометрической прогрессии – это нечто абстрактное и оторванное от жизни. На самом деле множество экономических процессов построены именно на основе геометрической прогрессии.
Например, если вы положите деньги на банковский депозит и захотите посчитать сколько процентов заработаете за три года, самым удобным способом провести вычисления будет именно через формулу геометрической прогрессии. Этот инструмент также применяется в проектировании, архитектуре и строительстве.
В этом тексте вы сможете узнать базовую информацию о формулах и свойства геометрической прогрессии, а также понять принцип, по которому она действует.
Что такое геометрическая прогрессия?
3, 12, 48, 192, 768, 3072 – это пример геометрической прогрессии. Все эти объединенные единым общим множителем. В теории геометрической прогрессии он называется знаменателем и обозначается как q. В этом случае q = 4. Чтобы создать геометрическую прогрессию, нам нужно сначала три умножить на четыре, затем 12 – снова на 4, потом 48 на 4 и так далее.
Читайте также: Плюсы и минусы образования за рубежом
Определение геометрической прогрессии
Геометрическая прогрессия – это прежде всего последовательность чисел. Каждый пункт этой последовательности, начиная со второго, равен предыдущему числу, умноженному на одинаковый множитель.
Устойчивое число множитель, которое собственно и образует последовательность под названием геометрическая прогрессия, называется знаменателем прогрессии и обозначается, как мы уже отметили выше, буквой q.
Члены прогрессии обозначаются как 
Предполагается, что ни первый член, ни знаменатель прогрессии не равен нулю.
Свойства геометрической прогрессии
Геометрическая прогрессия становится удобным инструментом вычислений, когда вы понимаете, что с помощью ее свойств и связанных с ней формул можно легко вычислить, чему равно
И действительно – если попробуем вручную умножать каждое число ряда на 4, в конце концов восьмым числом этой геометрической прогрессии станет 49152.
После усвоения главного принципа, лежащего в основе геометрической прогрессии, можем закрепить знания, проверив на практике первый пример с банковским депозитом.
Допустим, вы кладете на свой счет $ 100 под 6% годовых, и хотите узнать, какую сумму получите за 3 года. В таком случае вы будете использовать в своих расчетах геометрическую прогрессию, ведь ежегодно вы будете умножать все большую сумму на один и тот же множитель (в данном примере он равен 6%, то есть – 1,06)
Чтобы вычислить сумму вклада в момент завершения действия депозита, используем уже знакомую формулу для нахождения значения любого члена прогрессии:
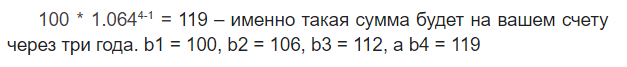
В чем разница между геометрической и арифметической прогрессией?
В геометрической прогрессии члены прогрессии умножаются на постоянное число, тогда как арифметическая прогрессия воплощает последовательность чисел, в которой к каждому предыдущему члена добавляется одно и то же постоянное число.
Представим это на примерах.
Предположим, что знаменатель (q) в случае геометрической прогрессии составит 3 и так же в арифметической прогрессии устойчивое слагаемое будет равно 3. И стартовый член прогрессии в обоих случаях также составит одно и то же число – 4.
Арифметическая прогрессия тогда будет выглядеть как последовательность 4, 7 (= 4 + 3), 10 (= 7 + 3) .., 13 .., 16 .., 19 ...
А геометрическая прогрессия – как последовательность 4, 12 (= 4 * 3), 36 (= 12 * 3), 108 .., 324 …
Читайте также: Учимся играя. Что такое геймификация
Формулы и свойства геометрической прогрессии
Свойства членов геометрической прогрессии – это формулы, упрощающие расчеты. Вот некоторые из них:
Чтобы найти знаменатель геометрической прогрессии, следует использовать следующую формулу:
Произведение членов, равноудаленных от краев геометрической прогрессии, то есть, соседних, всегда является постоянной величиной, то есть:
С формулой расчета любого члена геометрической прогрессии мы уже знакомы. Она выглядит так:
А формула нахождения суммы п первых членов геометрической прогрессии выглядит так:
Любой член геометрической прогрессии, начиная со второго, будет равняться среднему арифметическому соседних с ним членов, то есть при 
Калькуляторы геометрической прогрессии
В сети есть множество калькуляторов как арифметической, так и геометрической прогрессии. Некоторые из них могут не только посчитать сумму прогрессии или найти знаменатель, но и отразить пошаговое решение того или иного примера. Пользуясь ими вы не только найдете ответ, но и сможете понять принцип действий и запомнить некоторые из формул.
Однако если вы переживаете сложности с пониманием геометрической прогрессии, эффективным решением может быть работа с репетитором по алгебре. На сайте БУКИ вы можете найти репетитора по любому предмету.
Что касается онлайн-калькуляторов прогрессии, то в Keisan Online Calculator вы можете вычислить или сумму геометрической прогрессии, а также значение любого ее члена с пошаговым решением вашего примера. А в Geometric Sequence Calculator вы сможете вычислить любой составляющая прогрессии: и знаменатель геометрической прогрессии (q), и сумму бесконечный прогрессии (Sn), и сумму первых членов (Sn).
Примеры решения заданий с геометрической прогрессией
-
Вычислим знаменатель геометрической прогрессии, если b1=5,5; b2=11.
Решение:
Вычислим знаменатель прогрессии, поделив друг на друга соседние члены:
q = b2/b1 = 11/5,5 = 2.
Ответ:
Знаменатель прогрессии (q) равен 2.
-
Вычислим знаменатель геометрической прогрессии, если b1=0,3; b2= -30.
Решение:
Вычислим знаментель прогрессии, поделив друг на друга соседние члены:
q = b2/b1= -30/0,3= -100.
Ответ:
Знаменатель прогрессии (q) равен -100.
