Логарифмы традиционно считаются сложной темой в математике, однако созданы они были именно для того, чтобы облегчать расчеты. Если раньше ученики старших классов могли просто проигнорировать эту тему, то с введением обязательного ВНО по математике, логарифмы необходимо понимать и уметь использовать.
Рассказываем, что это такое и почему это не так сложно, как кажется.
Что такое логарифм?
Логарифм – это функция двух переменных, то есть степень, в которую надо возвести основание, чтобы получить аргумент.
Звучит сложно, но дальше будет проще. Расшифруем определение в классической формуле логарифма:
a – основа
x – аргумент
b – значение логарифма
Попробуем подставить простые значения, которые помогут понять принцип работы логарифма:
В какую степень надо возвести 2, чтобы получить 64? В 6.
Поэтому ответ будет:
Еще один пример для тренировки:
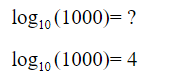
Это значит, что 1000 можно получить, если возвести 10 в 4 степень, то есть 4 раза умножить на себя.
Читайте также: Поступление в университет США: мечта или реальность
Для чего нужны логарифмы?
Логарифмы используются для упрощения подсчетов, когда речь идет об умножении больших цифр, а под рукой нет калькулятора. В давние времена, до повсеместного распространения компьютеров, логарифмы использовались для проведения расчетов в области строительства и черчения, в проектировании техники. А логарифмичные линейки и таблицы были неотъемлемыми инструментами архитекторов, математиков и инженеров.
Если у вас возникают сложности с пониманием логарифмов, хорошим решением станут занятия с репетитором по алгебре. Вместе вы сможете в вашем индивидуальном ритме усвоить каждое свойство логарифмов и проработать полученные знания на практике. Репетитора по любому предмету вы всегда можете найти на сайте Буки.
Попробуем более сложный пример, на котором будет более понятно истинное предназначение логарифмов. Умножим 42,5 на 378 с помощью логарифмической схемы. Для этого необходимо каждый из множителей представить в виде 10 в некоторой степени. Итак:
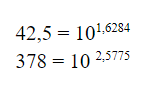
А значит, что:
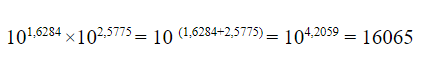
Попробуем записать пример с помощью логарифма, где 10 будет основой, а 4,2059 – логарифмом.
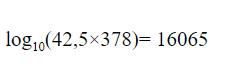
Если умножим 42,5 на 378 на калькуляторе или вручную и без использования логарифмов, получим то же значение – 16065.
Этот пример мы не могли бы решить логарифмично без знания определенных свойств логарифма, а именно – свойств десятичного логарифма и правила умножения логарифмов. Рассмотрим подробнее некоторые из главных свойств.
Читайте также: Как помочь ребенку подготовиться к ЗНО?
Свойства и формулы логарифмов
Логарифмы является удобным и легким способом проводить вычисления, если вы знаете свойства и формулы логарифмов. Все свойства являются действительными в случае, если a>0, a≠1, b>0, c>0
Логарифм единицы из любой основой равен нулю.
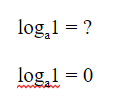
Так как в степени ноль равен единице 
Логарифм произведения равен сумме логарифмов.
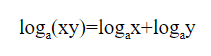
Логарифм суммы равна логарифму произведения.
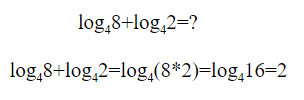
Логарифм деления равен разнице логарифмов.
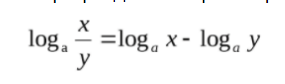
Логарифм вычитания равен частному логарифмов.
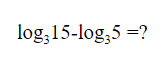
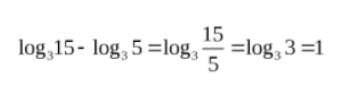
Логарифм степени равен произведению показателя степени, умноженного на логарифм основания.
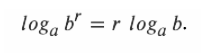
Онлайн-калькуляторы логарифмов
Вычислить логарифмы онлайн можно и с помощью стандартного калькулятора от Google. Однако есть и ряд специальных ресурсов, которые помогут и проводить логарифмические вычисления и решать другие математические задачи.
Например, на сайте Symbolab.com можно вычислять логарифмы с пошаговым решением конкретных примеров. Этот онлайн-калькулятор удивительно удобен, если вы хотите отработать свои навыки или на примерах любой сложности понять, как функционируют логарифмы. Кроме того, множество других типичных математических вычислений вместе с пояснениями доступны на сайте бесплатно.
На мультифункциональном сайте RapidTables вы также сможете найти бесплатный и удобный, хотя и более упрощенный, чем в предыдущем калькуляторе, инструмент для вычисления логарифмов.
Не только онлайн-калькулятор логарифмов, но и перечень стандартных логарифмических свойств вы можете найти на сайте Calculator.net в разделе Log calculator.
