Щоб зрозуміти в якому стані математична освіта України, звісно, найкраще було б подивитися як одні і ті ж самі задачі розв’язують учні в нас та закордоном. Однак, якщо це неможливо, то інформативним може бути, навіть, порівняння рівня складності задач, які пропонуються на аналогах ЗНО в інших державах. У якості прикладу візьмемо Польщу – нічим непримітну (в плані математичної освіти) країну-сусідку. У Польщі учні цього року вже написали матуру (аналог нашого ЗНО) з математики. Подібно до нашого ЗНО, матуру учні здають на двох рівнях – рівні стандарту (podstawowy) та на профільному (rozszerzony) рівні. Не хочу наперед робити висновки про рівень складності польських задач, а тому просто починаємо по порядку розв’язувати задачі матури-2022 профільного рівня, нічого не пропускаючи (як кажуть у юриспруденції, нічого не приховуючи і нічого не спотворюючи). Ці задачі є найпростішими (кількість балів за кожну задачу вказана в дужках після номера задачі).
У першій задачі необхідно обчислити значення виразу log₃√̅2̅7̅ – log₂₇√̅3̅. Матимемо, що log₃√̅2̅7̅ – log₂₇√̅3̅ = (3/2)log₃3 – (1/3)(1/2)log₃3= 3/2 – 1/6= 4/3.

У другій задачі необхідно обчислити значення похідної функції f(x)=(x³–8)/(x–2) у точці х=1/2. Матимемо, що похідна f´(x)= (3x²(х–2)–(x³–8))/(x–2)² = (2x³–6х²+8)/(x–2)². Тоді f´(1/2)=3.
У третій задачі відомо, що cos β = –1/3 та β є (π; 3π/2), а необхідно обчислити sin(β – π/3). Оскільки, cos β = –1/3, то sin²β= 1– cos²β= 1–1/9= 8/9. Оскільки, β є (π; 3π/2), то sinβ<0. Тоді sinβ= – (2/3)√̅2̅ . Тоді sin(β – π/3)= sinβ‧cos(π/3) – cosβ‧sin(π/3)= – (2/3)√̅2̅ ‧(1/2) – (–1/3)‧(√̅3̅ /2)= (√̅3̅ –2√̅2̅ )/6.

Задача №4. В першій урні є одна біла кулька та 6 чорних, а в другій урні – чотири білі кульки та три чорні. Підкидаємо симетричну монету. Якщо випаде решка, то навмання виймаємо одну кульку з першої урни. У протилежному випадку навмання виймаємо одну кульку з другої урни. Необхідно обчислити ймовірність того, що вийнята кулька виявиться білою. Шукана ймовірність рівна (1/2)‧(1/7) + (1/2)‧(4/7)= 5/14.

У п’ятій задачі дано послідовність aₙ=((7p–1)n³+5pn–3)/((p+1)n³+n²+p) при n≥1, де р – деяке додатне дійсне число. При якому значенні р границя цієї послідовності дорівнює 4/3? Насамперед неважко обчислити, що ця границя рівна (7р–1)/(р+1). Тоді (7р–1)/(р+1)=4/3, звідки р=7/17.
У задачі №6 необхідно довести, що для довільного дійсного числа х та для довільного дійсного у такого, що 2x>y, виконується нерівність 7x³+4x²y ≥ y³+2xy²–x³. Ця нерівність рівносильна такій нерівності: 8x³+4x²y ≥ y³+2xy² ↔ 4x²(2х+у) ≥ y²(2х+у) ↔ (4x²– y²)(2х+у) ≥ 0 ↔ (2x–y)(2х+у)² ≥ 0.
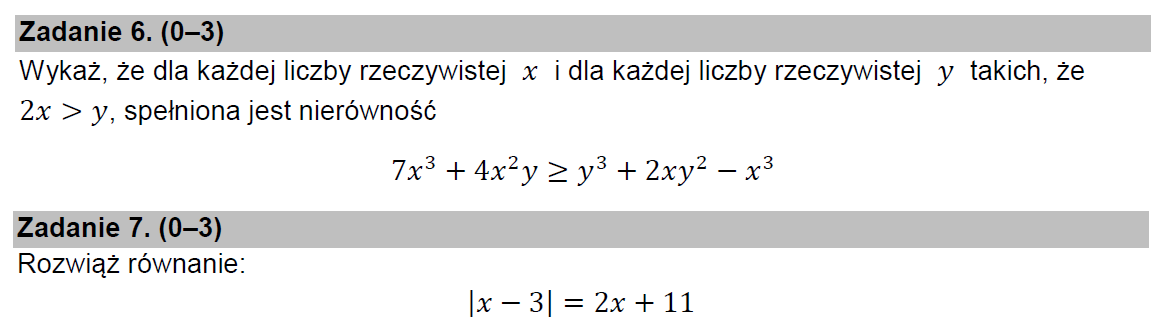
Стандартно розв’язується рівняння з модулем з сьомої задачі. Відповідь: є один корінь х= –8/3.
Два способи розв’язання є в такої задачі.
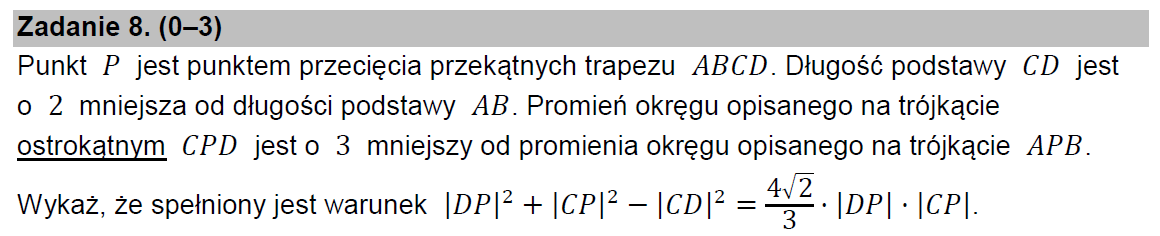
Нехай P – точка перетину діагоналей трапеції ABCD, основа CD якої на 2 менша за основу АВ. Радіус кола описаного навколо гострокутного трикутника CРD на 3 менший за радіус кола описаного навколо трикутника АВР. Слід довести, що DP²+CP²–CD²=(4/3)√̅2̅ ‧DP‧CP. Для зручності, позначимо АВ=а, а кут CРD позначимо як φ. Тоді CD=а–2. Нехай R – радіус кола, описаного навколо трикутника АВР. Тоді (R–3) – радіус кола, описаного навколо трикутника CРD. Тоді з трикутників АВР та CРD, по теоремі синусів отримаємо, що: a/sinφ=2R та (a–2)/sinφ=2(R–3). Поділивши почленно ці рівності одна на одну, отримаємо: (а–2)/а=(R–3)/R, звідки R=1,5а. Тоді sinφ=а/(2R)=1/3. Тоді cos²φ= 1– sin²φ= 1–1/9= 8/9. Оскільки, кут φ гострий, то cosφ=(2/3)√̅2̅ . По теоремі косинусів, DP²+CP²–CD²=2cosφ ‧DP‧CP=(4/3)√̅2̅ ‧DP‧CP. Зауважте, що ми ніде не користувались тим, що ABCD – трапеція. Якби ми цим скористались, то рівність (а–2)/а=(R–3)/R випливала б з подібності трикутників АРВ та CРD.
Задача №9. Остача від ділення многочлена W(x)=4x³–6x²–(5m+1)x–2m на двочлен х+2 дорівнює –30. Треба обчислити m і для цього значення m розв’язати нерівність W(x)≥0.

Матимемо, що W(x)=4x³–6x²–(5m+1)x–2m= 4x²(x+2)–14x²–(5m+1)x–2m= 4x²(x+2)–14x(x+2)–(5m–27)x–2m= 4x²(x+2)–14x(x+2)–(5m–27)(x+2)+2(5m–27)–2m= (x+2)(4x²–14x–5m+27)+8m–54. Тому 8m–54= –30, звідки m=3. Тоді W(x)=4x³–6x²–16x–6. Розв’язуємо нерівність 4x³–6x²–16x–6 ≥0. Скоротивши її на 2, отримаємо: 2x³–3x²–8x–3 ≥0. Можна помітити, що при х=–1 многочлен 2x³–3x²–8x–3 дорівнює нулю. Тому цей многочлен без остачі ділиться на двочлен (х+1). Маємо, що 2x³–3x²–8x–3= 2х²(х+1)–5x²–8x–3= 2х²(х+1)–5x(х+1)–3x–3= (х+1)(2х²–5x–3). Неважко отримати, що 2х²–5x–3=2(х–3)(х+0,5). Тоді наша нерівність набуває вигляду 2(х–3)(х+0,5)(х+1) ≥0. Тому х є [–1; –0,5]U[3; +∞).
Зауважте, що ми поки що ще не розв’язували найскладніших задач польської матури-2022 (про них в окремому блозі поговоримо). Хоча розглянуті вище задачі не є дуже складними, а деякі – відносно прості, але вже видно, що на нашому ЗНО профільного рівня є багато значно простіших задач. Більше того, цього року польська матура була простішою, ніж в попередні роки. Приміром, 2021-го року на польській профільній матурі три найпростіші (однобальні) задачі були такими:
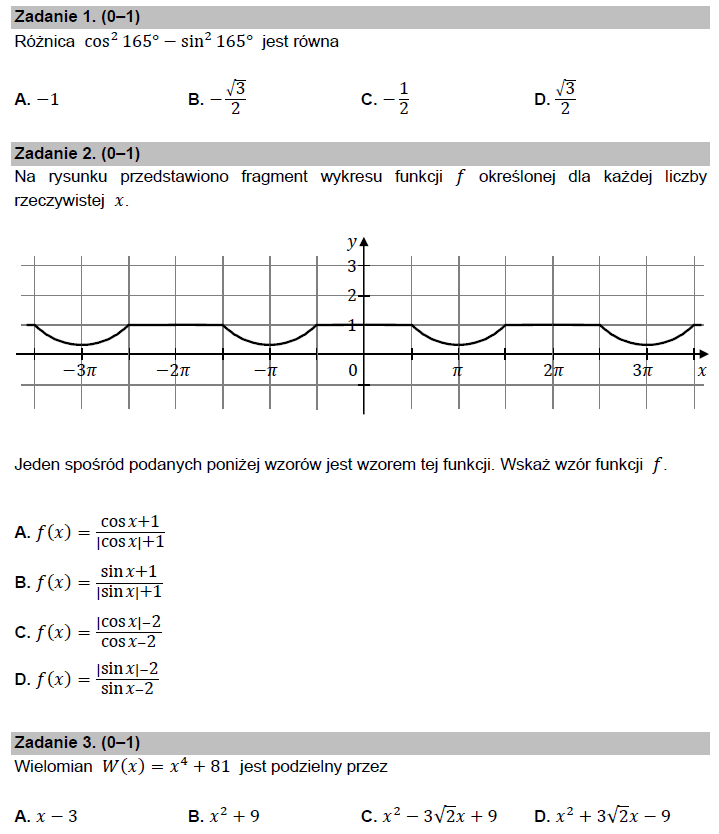
У першій задачі необхідно було обчислити значення виразу, у другій – серед запропонованих варіантів вказати функцію, графік якої зображено на рисунку. Ну, а в третій задачі потрібно було здогадатись, що многочлен х⁴+81 без остачі ділиться на многочлен х² –3√̅2̅ ‧х +9.
Не хотілось би зараз говорити про, м’яко кажучи, примітивний рівень задач нашого ЗНО з математики профільного рівня (це буде ще чіткіше видно з аналізу найскладніших задач матури-2022). Радше, цей блог є відповіддю тим, хто хотів би спрощення шкільної математики в Україні. Нема куди вже спрощувати…





