Тригонометричні формули: що потрібно знати для НМТ з математики і не тільки

Тригонометричні функції, такі як синус, косинус, тангенс і котангенс, потрібні не лише для розв’язання теоретичних задач. Адже вони пов’язані з вимірюванням кутів, а ця навичка необхідна в багатьох професійних галузях: архітектурі, мистецтві, медицині, автомеханіці, дослідженні природних явищ, наприклад, заломлення світла. 

НМТ містить значний пласт завдань, що базуються на тригонометрії. Тож учні повинні приділяти особливу увагу цьому розділу, і добре засвоїти ази — значення тригонометричних функцій. Взагалі готуватися до тесту з математики краще за підтримки професійного репетитора. На BUKI знайти такого фахівця можна за кілька хвилин, застосувавши пошукові фільтри. 

Стаття корисна для учнів шкіл та майбутніх вступників, що готуються до НМТ. У ній зібраний вичерпний матеріал про всі тригонометричні формули і функції, а також їх практичне застосування для розв’язання задач.

Що таке тригонометрія та чому тригонометричні формули важливі для НМТ?

Такий розділ математики, як тригонометрія, школярі зазвичай починають вивчати у 10 класі. Знайомство з розділом починається з теми «Синус, косинус, тангенс, котангенс кута». Власне, сам розділ досліджує співвідношення між сторонами й кутами трикутників. 

Вперше способи розв‘язування трикутників були знайдені давньогрецькими астрономами Гіпархом та Клавдієм Птолемєєм. 

Ось які теми з тригонометрії виносяться на НМТ:

• Означення синуса, косинуса, котангенса числового аргументу
• Основні співвідношення між тригонометричними функціями одного аргументу
• Формули зведення
• Формули додавання та наслідки з них
• Методи розв’язання найпростіших тригонометричних рівнянь
• Тригонометричні функції та їх основні властивості

Учасник тестування, згідно зі стандартами Програми НМТ-2026 щодо практичних навичок, повинен вміти:

• виконувати тотожні перетворення тригонометричних виразів та знаходити їх числове значення за заданих значень змінних
• розв’язувати найпростіші рівняння, що містять тригонометричні вирази
• розв’язувати нерівності, що містять тригонометричні вирази
• користуватися графічним методом розв’язування рівнянь, нерівностей та їх систем
• застосовувати рівняння, нерівності та системи рівнянь до розв'язування текстових задач
• будувати графіки тригонометричних функцій
• використовувати перетворення графіків функцій

Тема тісно пов’язана з такою сферою математики, як геометрія. Обчислення кутів і лягло в основу формул тригонометрії. 

Основні тригонометричні функції: синус, косинус, тангенс, котангенс

Дамо означення синуса й косинуса через кути прямого трикутника:

• Синус в прямокутному трикутнику синус гострого кута визначається як відношення протилежного катета до гіпотенузи.
• Косинус — це відношення прилеглого катета до гіпотенузи в прямокутному трикутнику.

Ці співвідношення легше уявити за допомогою малюнка, де α — це гострий кут, а — протилежний до нього катет трикутника, b — прилеглий до нього катет трикутника, с — гіпотенуза трикутника. 

Дамо визначення ще двом функціям:

• Тангенс — це відношення довжини протилежного катета до довжини прилеглого катета.
• Котангенс — це відношення довжини прилеглого катета до довжини протилежного катета.

Розглянемо їх за допомогою кута та формул.

Графічні матеріали взяті з навчальної платформи МійКлас. 

Таблиця тригонометричних функцій 

Розпочнемо із загальних значень. 

У таблиці дано означення sin та cos через відношення сторін трикутника. А означення tg і ctg подано як через відношення сторін трикутника, так і через співвідношення sin і cos. 

Таблиця значень тригонометричних функцій для кутів 0°, 30°, 45°, 60°, 90°

Це база для учнів, які тільки почали вивчати тригонометричні функції. 

Повна таблиця тригонометричних функцій для кутів від 0° до 180° з кроком в 1° міститься на сайті ФінКалк. 

Як запам’ятати таблицю тригонометричних функцій швидко та ефективно?

Насамперед важливо використовувати наочні зображення. Так, візуалізація кутів допомагає утримати формули в пам’яті значно довше, ніж зубріння. Спробуйте зрозуміти:

• 30° і 60° – це кути у прямокутному трикутнику 1–√3–2
• 45° – рівнобедрений трикутник зі сторонами 1–1–√2

Це, до речі, не єдиний спосіб дієвого запам’ятовування. Ось ще кілька:

1. Техніка мнемонічних фраз. Підходить для вивчення закономірностей. Наприклад, «синус росте з нуля, а косинус спадає з одиниці». 

Ще одна закономірність: таблиця синусів і косинусів — дзеркальна. 

• sin(0°) = 0 ↔ cos(90°) = 0
• sin(30°) = 1/2 ↔ cos(60°) = 1/2
• sin(45°) = √2/2 ↔ cos(45°) = √2/2

Якщо запам’ятати sin, то cos можна просто «прочитати у зворотному порядку».

1. Використовуйте квадратну закономірність. Синуси кутів 0°, 30°, 45°, 60°, 90° можна подати простою формулою:

sin(α) = √n/2, де n = 0, 1, 2, 3, 4. 

А косинуси — у зворотному порядку: cos(α) = √4-n/2.

Це дозволяє не вчити всю таблицю, а лише послідовність чисел 0, 1, 2, 3, 4.

Всі тригонометричні формули, які потрібно знати

Для практичної роботи над завданнями школярам потрібно знати 7 типів формул. 

Основні тотожності тригонометрії

«Золотим правилом» тригонометрії вважається тотожність: sin²α + cos²α = 1.

Звідси випливає, що якщо відомо sin α, то cos α можна знайти як: cosα = √1 – sin²α. 

Наприклад, якщо sinα = 3/5, то cosα = √1 – (3/5)2 = 4/5.

Тотожності для тангенса і котангенса

Ці формули пов’язують tg і ctg із sin і cos: 

tanα = sinα/cosα, cotα = cosα/sinα.

Звідси випливає, що: tanα ⋅ cotα = 1.

Наприклад, якщо sin α = 3/5, cos α = 4/5, то tanα = 3/5 : 4/5 = 3/4; cotα = 4/3.

Формули додавання та різниці: sin(a ± b), cos(a ± b), tg(a ± b), ctg(a ± b)

Базові тригонометричні формули включають:

• Формулу синуса суми: sin(a+b) = sina⋅cosb+cosa⋅sinb

• Формулу косинуса суми: cos(a+b) = cosa⋅cosb−sina⋅sinb

• Формулу синуса різниці: sin(a−b) = sina⋅cosb−cosa⋅sinb

Вона була виведена з формули синуса суми на основі властивості парності функції косинуса і непарності функції синуса. 

• Формулу косинуса різниці: cos(a−b) = cosa⋅cosb+sina⋅sinb

Вона була виведена з формули косинуса суми на основі властивості парності функції косинуса і непарності функції синуса. 

Формули суми та різниці для тангенса: 

У цих формулах виражено співвідношення між тангенсом загальної суми або різниці аргументів і тангенсами окремих аргументів — доданків.

При цьому для всіх тангенсів виконуються умови:

Формули суми та різниці для котангенса виводяться наступним чином:

Приклад практичного застосування формул. Потрібно обчислити вираз cos110°⋅cos20°+sin110°⋅sin20°.

Цей вираз нагадує формулу косинуса різниці кутів: cos(a−b) = cosa⋅cosb+sina⋅sinb.

За цією формулою, маємо cos110°⋅cos20°+sin110°⋅sin20° = cos(110°−20°) = 90°.

Отже, cos(110°−20°) = cos90°. А cos90° = 0. 

Формули подвійного та потрійного аргументу

Формули для подвійного кута — це ряд формул, які допомагають виразити тригонометричні функції кута 2x через тригонометричні функції того ж кута x. Тобто, по суті, ці тригонометричні формули спрощують розв’язання складних рівнянь і зводять обчислення до базових формул, наприклад, синуса суми. 

Формули потрійного кута дозволяють знайти значення синуса, косинуса та тангенса кута, кратного трьом із використанням значення цих функцій для вихідного кута. 

Формули пониження степеня: sin²a, cos²a, tg²a, ctg²a

Формули пониження степеня (або формули зведення квадратів тригонометричних функцій) допомагають виражати квадрати синуса, косинуса, тангенса і котангенса через функції одинарного кута.

Це дуже зручно, коли треба спростити тригонометричні вирази або інтегрувати тригонометричні функції. Їх виводять з основної тригонометричної тотожності:

cos2a = cos2a−sin2a = 1−2sin2a = 2cos2a−1.

Формули перетворення добутку в суму і різницю

Ми використовуємо формули суми і різниці кутів, щоб замінити добутки на суму або різницю синусів чи косинусів. Це необхідно для спрощення обчислень.

Ключові формули для tg і ctg

Як зазначалось вище, тангенс — це відношення синуса до косинуса. При цьому значення кута має підлягати умові: α ≠ π/2 + πn, n є Z. 

Звідси маємо ще одну формулу: 1 + tg2α = 1/cos2α.

Котангенс — це відношення косинуса до синуса. При цьому кут α ≠ π + πn, n є Z.

Маємо ще одну формулу для котангенса: 1 + ctg2α = 1/sin2α.

Наприклад, потрібно обчислити вираз (1+ctg2α)sin2α. 

Підставимо його в формулу: (1+ctg2α)sin2α = 1/sin2α ⋅ sin2α = 1. 

Як застосовувати тригонометричні формули на практиці? 

Тригонометричні функції допомагають розуміти, як змінюються сторони трикутника, коли ми змінюємо його кути. Це дозволяє вирішувати різні завдання, такі як вимірювання відстаней, висот будівель, кутів на карті тощо.

Наприклад, якщо ми маємо прямокутний трикутник і знаємо один кут та довжину однієї зі сторін, можна за допомогою тригонометрії встановити довжину іншої сторінки цього трикутника. 

Розглянемо на прикладі значень для фізики. Гармонічні коливання в природі або техніці відбуваються за законами синуса або косинуса. 

• В електромагнітної хвилі вектор напруженості електричного поля Е і магнітної індукції В змінюються по синусоїдальному закону, взаємно перпендикулярні один одному і напряму розповсюдження хвилі. 
• Ще один приклад синусоїдальних коливань — звук. Про значення застосування радіохвиль годі й говорити. Це основа для телебачення та зв’язку з космічними супутниками. 

Найбільш зручним математичним методом для дослідження коливних процесів є тригонометричні функції. Ось рівняння гармонічного коливання, де тригонометричні формули допомагають знаходити амплітуду, період, фазу руху: x = Asin(ωt+φ).

Крім цього, в тригонометрії формули використовують для: моделювання руху, створення 3D-графіки та анімацій.

Також пілоти, моряки й топографи використовують синуси та косинуси для розрахунку напрямків, відстаней між точками на сферичній поверхні Землі, навіть у системах GPS.

Тригонометричні формули допомагають вимірювати відстані, кути та висоти, коли це неможливо зробити напряму. Наприклад, знаючи кут підйому на гору й відстань до неї, за формулою h = d⋅tanα можна знайти висоту h. До того ж у проєктуванні будівель і мостів обчислюють нахили, довжини перекриттів та кутові з’єднання.

Формули тригонометричних рівнянь

Тригонометричне рівняння — це рівняння, у якому невідоме знаходиться всередині тригонометричної функції: sinx, cosx, tanx, cotx. Наприклад: sinx = 1/2; cos2x = 0; 2sinx – √3 = 0. 

Формули тригонометричних рівнянь включають обернені тригонометричні функції. 

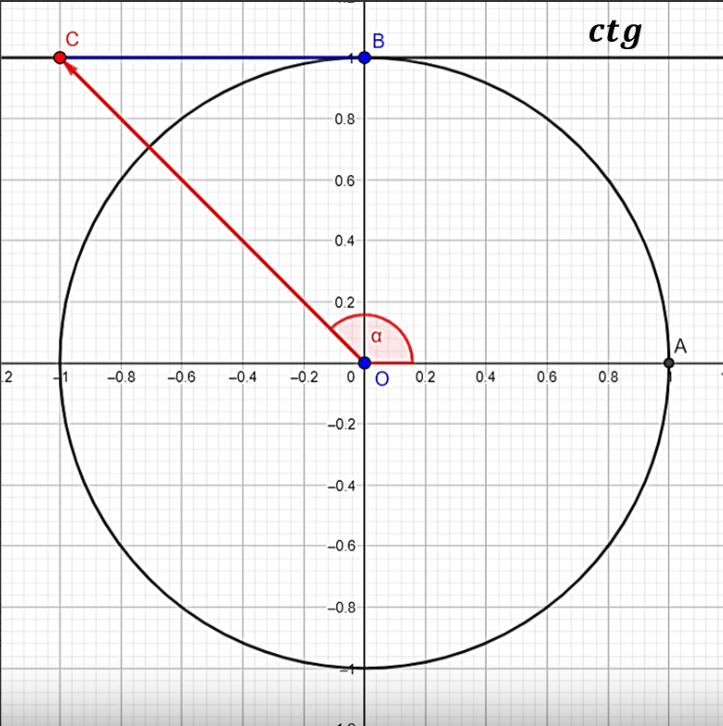
Для синуса: sin(α) = a, звідси α = (−1)k arcsin(a) + πk, k ∈ Z. 

Або x = arcsina+2πn, x = π−arcsina+2πn.

Для косинуса: cos(β) = a, звідки β = ±arccos(a)+2πn, n ∈ Z.

Тобто x = arccosa+2πn; x = −arccosa+2πn.

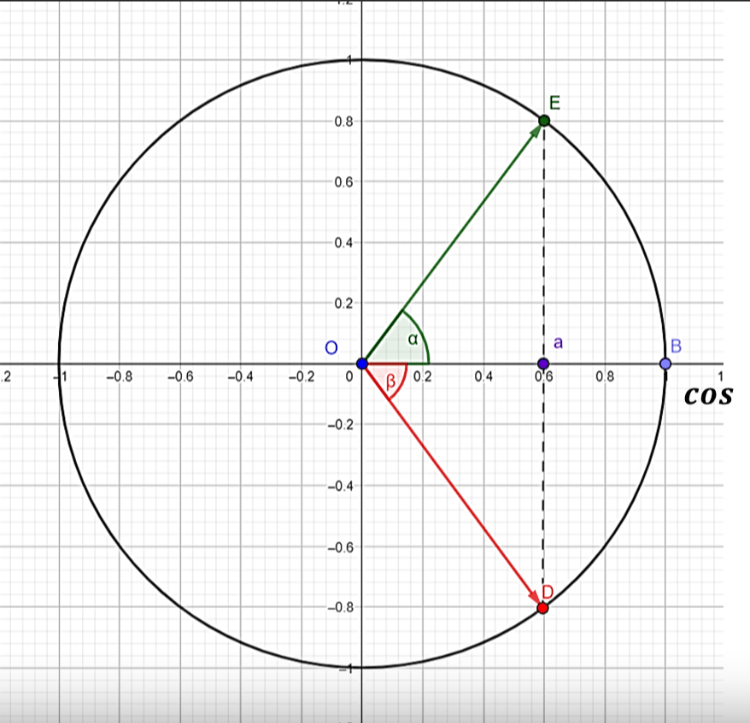
Для тангенса: tgα = b, звідси α = arctgb+πk, k ∈ Z.

Тангенс має період π.

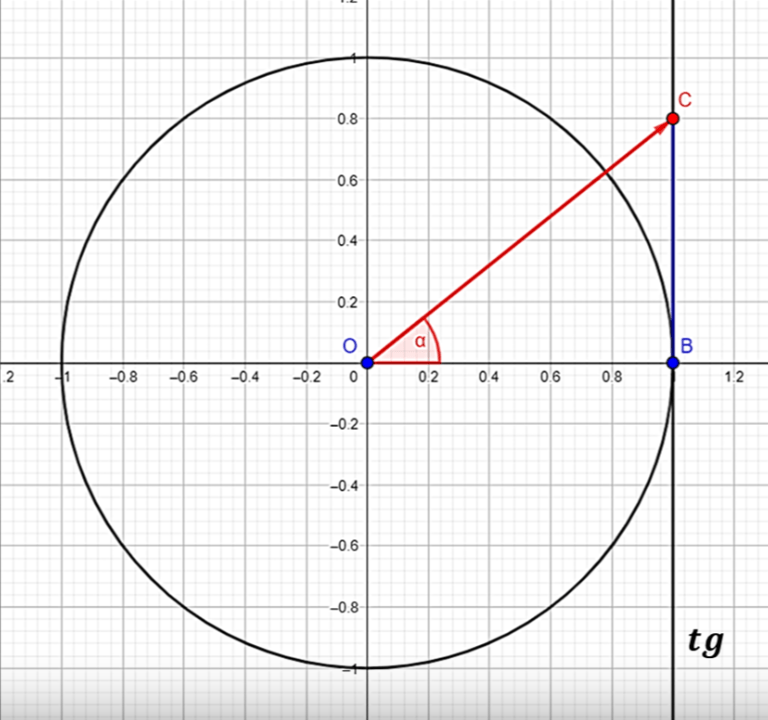
Для котангенса: ctgβ = a, звідки β = arctga+πn, n ∈ Z.

Ми розглянули 4 формули для найпростіших рівнянь. 

Звернімо також увагу на особливості рівнянь, якщо α = 0, 1, –1. 

Складні тригонометричні рівняння потрібно зводити до простих з однією функцією або одним аргументом. Серед інших методів розв’язання таких рівнянь визначають розкладання на множники, заміну змінних, зведення до однорідних рівнянь. 

Приклади розв’язання типових тригонометричних рівнянь

У цьому розділі проаналізуємо розв’язання рівнянь, які входили до завдань НМТ за 2022–2025 роки. 

Рівняння 1: sin4x = –1.

Розв’язання: 

sinα = −1.

Це рівняння виконується тоді, коли кут α дорівнює:

α = 3π/2 + 2πn, n ∈ Z. Адже синус дорівнює –1 у точці 3π/2 і повторюється через 2π. 

Підставляємо α = 4x, 4x = 3π/2 + 2πn.

Щоб знайти х, поділимо обидві частини на 4: х = 3π/8 + πn/2, n ∈ Z.

Рівняння 2: cos(3x) = 1/2.

Розв’язання: 

Рівняння cos x = a при |а| < 1 має розв’язок ±arccos(a)+2πn, n ∈ Z.

Отже, 3x = ±arccos1/2 + 2πn, n ∈ Z.

3x = ±π/3 + 2πn, n ∈ Z.

x = ±π/9 + 2πn/3, n ∈ Z.

Рівняння 3: tg(3x) = – 1. 

Розв’язання: 

3x = arctg (– 1) + sin πn, n ∈ Z.

3x = – π/4 + πn, n ∈ Z.

x = – π/12 + πn/3, n ∈ Z.

Рівняння 4: Визначте найменше значення а, за якого має корені рівняння:

sin x + π/3 = 2a2 + 5a – 6. 

Розв’язання: 

Дане тригонометричне рівняння має корені, якщо задовольняє параметр |2a2 + 5a – 6| ≤ 1. 

Маємо розв’язати систему нерівностей другого степеня. 

Щоби знайти ще два значення а, потрібно розв’язати квадратне рівняння. 

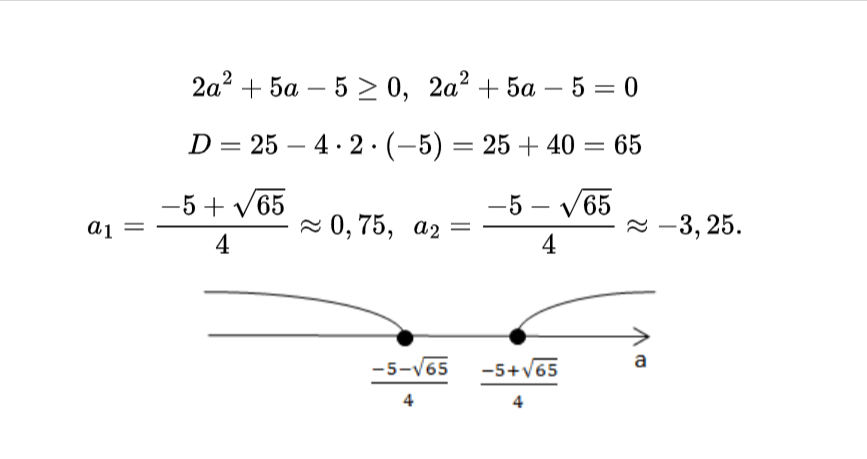
Всі розв’язки системи: –3,5; –3,25; 0,57; 1. 

Найменшим значенням а є –3,5. 

Підготовка до НМТ: як ефективно повторити тригонометрію

Тригонометричні функції можуть бути представлені у завданнях мультитесту по-різному:

• на визначення довжини сторони трикутника чи прямокутника
• на узгодження виразів з твердженнями про їхнє значення
• на спрощення виразів (наприклад, (1 – sin2 α) ⋅ tg2 α))
• на співвіднесення функції з її властивостями
• на тотожність тригонометричних виразів
• у складі тригонометричних нерівностей та їх систем
• на обчислення значення виразу з синусом, якщо відоме значення цього виразу з косинусом і навпаки

Тож радимо розв’язувати якомога більше таких завдань. Для цього можете скористатися тренувальними тестами на порталі osvita.ua зразками тестів за минулі роки. Працюйте із тригонометричною таблицею чи не кожен день, розв’язуючи типові рівняння. 

Аби надійно засвоїти матеріал, важливо вчити не формули, а взаємозв’язки. Замість того щоб зубрити, намалюйте коло одиничного радіуса:

• відкладайте кути в градусах і радіанах
• позначайте, де sin > 0, де cos < 0
• підписуйте типові значення (0°, 30°, 45°, 60°, 90°)

Це допомагає запам’ятати все через зорові образи і не плутати знаки в формулах.

А щоб підготуватися на найвищому рівні, краще знайти репетитора з математики для систематичних занять. Педагог, який спеціалізується на тренуванні до НМТ, зможе пояснити всі нюанси тестування та особливості завдань. Репетитор складе план повторення з урахуванням поточного рівня знань та часу, що лишився до іспиту. 

Висновок

Тригонометрія на шкільному рівні доволі зрозуміла, якщо вміти практично застосовувати формули, запам’ятати знаки функцій у чвертях, повторювати таблицю значень для стандартних кутів (30°, 45°, 60°).

Блок НМТ з математики може містити від 1 до 2–3 завдань на синус, косинус, рідше — тангенс чи котангенс. Складіть план підготовки за тренувальними вправами щонайменше на місяць, виконуйте до 20 практичних завдань на обчислення, спрощення виразів, тригонометричні рівняння, знаходження кута за значенням функції.

Якщо тема для учня складна й він чи вона припускається помилок у 50% завдань, варто підшукати репетитора для індивідуального пояснення тем.