Геометрична прогресія: пояснення та формули

Учням може здаватися, що вивчення геометричної прогресії – це щось абстрактне та відірване від життя. Насправді ж безліч економічних процесів побудовані саме на основі геометричної прогресії.

Зокрема, якщо ви покладете гроші на банківський депозит и захочете порахувати скільки відсотків заробите за три роки, найзручнішим способом провести обчислення буде саме формула геометричної прогресії. Цей інструмент також застосовується в проєктуванні, архітектурі та будівництві.

У цьому тексті ви зможете дізнатися базову інформацію про формули та властивості геометричної прогресії, а також зрозуміти принцип, за яким вона діє. 

Що таке геометрична прогресія?

3, 12, 48, 192, 768, 3072 – це приклад геометричної прогресії. Усі ці об’єднані єдиним спільним множником. У теорії геометричної прогресії сталий множник називається знаменником і позначається як q. У цьому випадку q = 4. Щоби утворити геометричну прогресію, нам потрібно спершу три помножити на чотири, потім 12 – знов на 4, потім 48 на чотири і так далі.  

Визначення геометричної прогресії

Геометрична прогресія – це передусім послідовність чисел. Кожен числовий пункт цієї послідовності, починаючи з другого, дорівнює попередньому числу, помноженому на сталий, незмінюваний множник. 

Стале число-множник, що власне і утворює послідовність під назвою геометрична прогресія, називається знаменником геометричної прогресії і позначається, як ми вже відзначили вище, літерою q. 

Члени прогресії позначаються як , де під індикатором n мається на увазі порядковий номер члена у прогресії. 

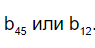
Передбачається, що ані перший член, ані знаменник геометричної прогресії не дорівнюють нулю. 

Читайте також: Навчаємося граючи. Що таке гейміфікація

Властивості геометричної прогресії

Геометрична прогресія стає зручним інструментом розрахунку, коли ви розумієте, що за допомоги її властивостей та пов’язаних із нею формул можна легко вирахувати, чого дорівнюватиме b45 чи b12. 

І дійсно – якщо спробуємо вручну множити кожне число ряду на 4, зрештою восьмим числом цієї геометричної прогресії стане 49152. 

Після засвоєння головного принципу, що лежить в основі геометричної прогресії, можемо закріпити знання, перевіривши на практиці перший приклад із банківським депозитом. Припустімо, ви кладете на свій рахунок $100 під 6% річних, і хочете дізнатись, яку суму одержите за 3 роки. У такому випадку ви будете використовувати у своїх розрахунках геометричну прогресію, адже щороку ви помножуватимете дедалі більшу суму на один і той самий множник (у цьому прикладі він дорівнюватиме 6%, тобто 1,06).

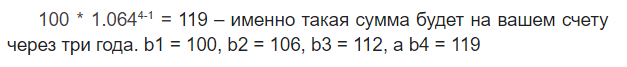
У чому різниця між геометричною та арифметичною прогресією?

У геометричній прогресії члени прогресії є помноженими на стале число, тоді як арифметична прогресія втілює послідовність чисел, у якій до кожного попереднього члена додається одне і те саме стале число. 

Представимо це на прикладах. 

Припустімо, що множник (q) у випадку геометричної прогресії становитиме 3 і так саме у арифметичній прогресії сталий доданок дорівнюватиме 3. І стартовий член прогресії у обох випадках також становитиме одне й те саме число – 4. 

Арифметична прогресія втілюватиметься тоді у послідовності 4, 7 (=4+3), 10 (=7+3).., 13.., 16.., 19...

Геометрична прогресія втілюватиметься у послідовності 4, 12 (=4*3), 36 (=12*3), 108.., 324…

Читайте також: Рейтинг вишів України за спеціальностями

Формули та властивості геометричної прогресії

Властивості членів геометричної прогресії – це формули, що спрощують розрахунки. От деякі з них: 

1. Щоби знайти знаменник геометричної прогресії, слід використати наступну формулу:

2. Добуток членів, рівновіддалених з кінців геометричної прогресії, тобто, сусідніх, є повсякчас сталою величиною, тобто:

.

3. Із формулою розрахунку будь-якого члена геометричної прогресії ми вже знайомі. Вона виглядає так:

.

4. А формула суми n перших членів геометричної прогресії виглядає так:

5. Будь-який член геометричної прогресії, починаючи з другого, буде дорівнювати середньому арифметичному сусідніх з ним членів, тобто при ,

;

Калькулятори геометричної прогресії

У мережі є безліч калькуляторів як арифметичної, так і геометричної прогресій. Деякі з них можуть не лише порахувати суму або знайти знаменник геометричної прогресії, а й відобразити покрокове рішення того чи іншого прикладу. Користуючись ними ви не лише знайдете відповідь, а й зможете зрозуміти принцип дій та запам’ятати деякі з формул. 

Однак якщо ви переживаєте складнощі із розумінням геометричної прогресії, ефективним рішенням може бути звернення до репетитора з алгебри. На сайті БУКІ ви можете знайти репетитора з будь-якого предмету. 

Що ж до онлайн-калькуляторів геометричної прогресії, то у Keisan Online Calculator ви можете вирахувати або суму геометричної прогресії, а також значення будь-якого її члена із покроковим рішенням вашого прикладу. А у Geometric Sequence Calculator ви зможете вирахувати будь-який складник прогресії: і знаменник геометричної прогресії (q), і суму нескінченний прогресії (Sn), і суму перших членів (Sn). 

Приклади рішення завдань із геометричною прогресією

2. Обчислимо знаменник геометричної прогресії, якщо b1=5,5; b2=11.

Розв'язання: Знаходимо знаменник прогресії

q=b2/b1=11/5,5=2.

Відповідь: знаменник прогресії (q) дорівнює 2.

3.Обчислимо знаменник геометричної прогресії, якщо b1=0,3; b2= -30.

Розв'язання: Знаходимо знаменник прогресії

q =b2/b1= -30/0,3= -100.

Відповідь: знаменник прогресії (q) дорівнює -100.

Читайте також: Найпопулярніші спеціальності у світі: вибір студентів 2021